- 直线的倾斜角与斜率
- 共186题
如图,已知椭圆



(1)求直线AB的方程;
(2)若点P为椭圆C上异于A、B的动点,且直线AP,BP分别交直线

[来源:学§科§网]
正确答案
见解析
解析
(1)设点E(m,m),由B(0,-2)得A(2m,2m+2)。
代入椭圆方程得

解得

所以A(

故直线AB的方程为
(2)设


设

∴
又点M在直线y=x上,解得M点的横坐标
设

∴
点N在直线y=x上,,解得N点的横坐标
所以OM·ON=

=


知识点
点
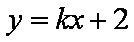




正确答案
-1或1
解析
略
知识点
已知直线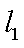
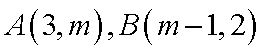
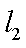
(1)当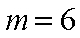
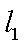

(2)若

正确答案
见解析
解析
解析:(1)当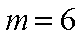


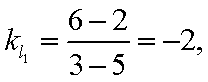
故 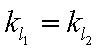
此时,直线
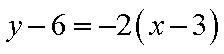

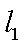
从而,
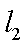
(2)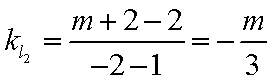

若
当

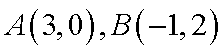

不符合题意,舍去;……………………………………………………………………..7分
当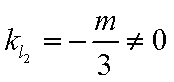



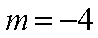
综上:
知识点
已知圆










(1)求直线
(2)求圆
正确答案
(1)
解析
解析:(1)由题意知:直线

故直线

(2)根据题意设: 


圆





解得:

圆

圆

知识点
已知椭圆E:
原点对称的两点,且直线PA的斜率与直线

(1)求E的方程;
(2)过E的右焦点作直线l与E交于M、N两点,直线MA、NA与直线



正确答案
见解析
解析
(1)设

又
故

(2)设直线MN的方程为
设
直线MA的方程为


得
所以
所以


故直线l的方程为
知识点
扫码查看完整答案与解析