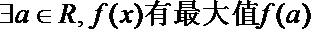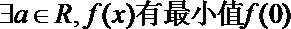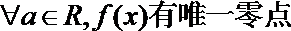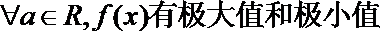- 分段函数的解析式求法及其图象的作法
- 共45题
9．已知函数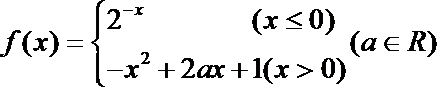
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12． 已知函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．已知函数
A
B
C
D0
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5．设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9.定义在R上的函数满足f(x)= 
正确答案
0
解析
由已知,得f(-1)=log22=1,f(0)=log21=0,f(1)=f(0)-f(-1)=-1,f(2)=f(1)-f(0)=-1,f(3)=f(2)-f(1)=-1-(-1)=0,f(4)=f(3)-f(2)=0-(-1)=1,f(5)=f(4)-f(3)=1,f(6)=f(5)-f(4)=0,…,故当x=1,2,3,4,0,…时,f(x)的取值依次是-1,-1,0,1,1,0,-1,-1,0,1,1,…,则f(x)是以6为周期的函数,故f(2016)=f(0)=0.
知识点
14.已知函数f(x)= 
正确答案
(-1,3)
解析
由分段函数可得f(f(1))=f(3)=6a+9,故f(f(1))>3a2⇒6a+9>3a2,解得-1<a<3.
知识点
14.已知函数f(x)= 
正确答案
(-1,3)
解析
由分段函数可得f(f(1))=f(3)=6a+9,故f(f(1))>3a2⇒6a+9>3a2,解得-1<a<3.
知识点
3.已知实数a≠0，函数f(x)=
A－
B
C－
D
正确答案
解析
当a>0时，2－2a+a=-1－a－2a，解得a=- 
当a<0时，-1+a－2a=2+2a+a，解得a=- 
知识点
4.已知函数f(x)=
正确答案
解析
f(x)=
由f(x)的图象（图略）可知f(x)在R上是单调递增函数
由f(2－a2)>f(a)，得2－a2>a
即a2+a－2<0，解得－2<a<1.
知识点
3.已知函数
A
B
C2
D4
正确答案
解析
由题可知：f(2)=-√2；f(-√2)= 
B选项不正确，C选项不正确，D选项不正确，所以选A选项。
考查方向
解题思路
本题考查分段函数的求值，解题思路如下：
依次代值计算即可
易错点
本题必须注意定义域的变化
知识点
扫码查看完整答案与解析