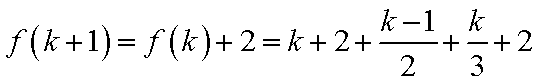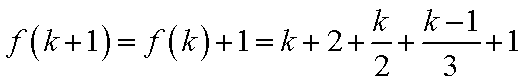- 数列与函数的综合
- 共73题
已知函数








17.分别求
18.记


正确答案
解析
由已知可得,an=f(n)=2n+1,即an=2n+1
因为bn=f(bn-1)=2bn-1+1
所以bn+1=2(bn-1+1)
所以数列bn+1是以首项为b1+1=2,公比为2的等差数列。所以
bn=2n+1
考查方向
构造法求数列的通项公式
解题思路
根据已知条件求出an,根据构造法判断数列bn+1为等比数列,进而求出bn
易错点
不会构造法
教师点评
本题主要考查数列通项公式和前问题,难度一般.求数列通项公式的常用方法有:公式法(包括等差数列的通项公式,等比数列的通项公式, ),累加法,累乘法,构造法等.数列求和的常用方法有:公式法,分组求和法,倒序相加法,裂项相消法,错位相减法.
正确答案
详见解析
解析
依题意,

当


所以
则


令

两式相减得
∴


∴
考查方向
错位相减法求数列的和
解题思路
根据定义知道小数部分,然后分析采用错位相减法求和
易错点
不会构造数列形式,不能想到利用错位相减法求和
教师点评
本题主要考查数列通项公式和前问题,难度一般.求数列通项公式的常用方法有:公式法(包括等差数列的通项公式,等比数列的通项公式, ),累加法,累乘法,构造法等.数列求和的常用方法有:公式法,分组求和法,倒序相加法,裂项相消法,错位相减法.
16.定义在




①

③令函数

④令数列

其中真命题的序号为 .
正确答案
①、②、③
解析
对于①:令


对于②:



对于③:令


对于④:
考查方向
本题考查了抽象函数及其应用
解题思路
令x=y=1,代入所给的式子求出f(1)的值,判断①真假;
令x=y=2,代入所给的式子,再结合数列的通项公式判断②真假;
令
利用

易错点
本题难度较大,考生容易由于不理解抽象函数、不会用赋值法而导致本题不会做。
教师点评
本体难度较大,综合性较强,需要考生扎实的基础知识和灵活的应变能力。
知识点
19. 设数列






(1)求证:数列

(2)令








正确答案
见解析
解析
解:(1)当


代入

而
∴数列
∴


又
(2)当



∴
故
当

若
则等式


若


∵



∴当且仅当


综上可知,当


当


考查方向
解题思路
利用

易错点
忽略n的范围的讨论。
知识点
23.已知集合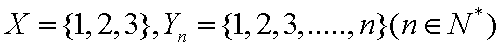

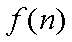
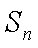
(1)写出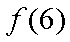
(2)当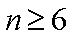
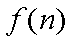
正确答案
(1)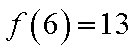
(2)当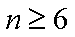
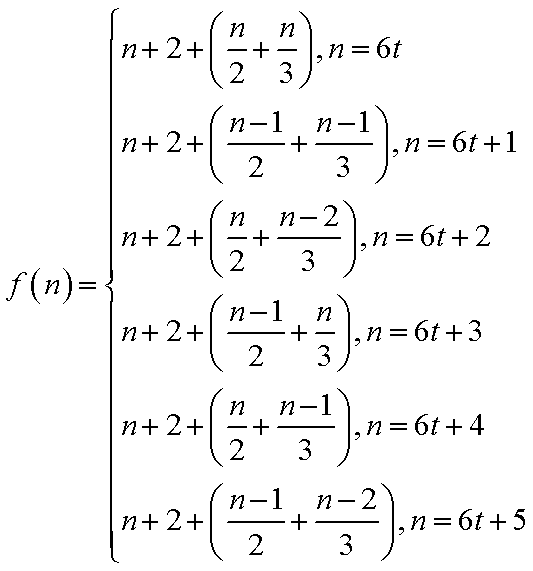
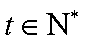
下面用数学归纳法证明:
①当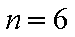
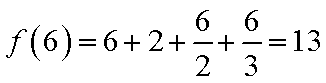
②假设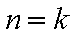
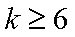
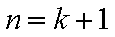
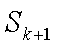
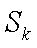
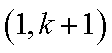
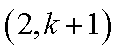
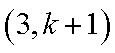
1)若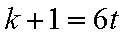
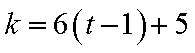
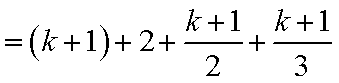
2)若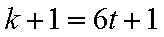
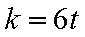
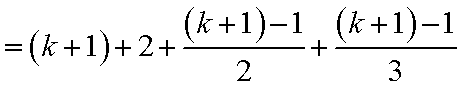
3)若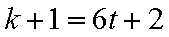
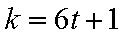
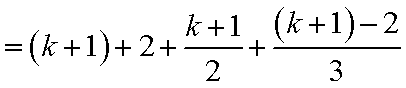
4)若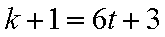
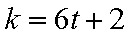
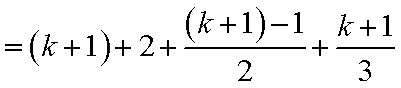
5)若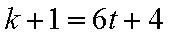
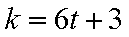
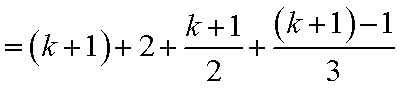
6)若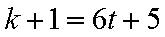
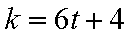
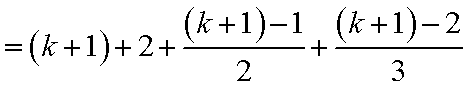
综上所述,结论对满足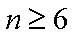
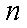
解析
解析已在路上飞奔,马上就到!
知识点
21.设








(1)证明:函数



(2)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列,其各项和为


正确答案
(1)
所以


又

所以


因为




(2)解法一:由题设,
设
当
当
若
若
所以


所以

综上所述,当


解法二 由题设,
当
当

当


假设

那么,当

又
令
所以当



当



所以
故

所以,对于一切

解法三:由已知,记等差数列为




所以
令
当


当
而


若


当


从而




所以当


综上所述,当


解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析