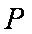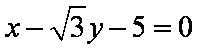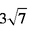- 点的极坐标和直角坐标的互化
- 共16题
已知曲线
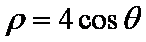
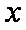

(1)求曲线
(2)设曲线



正确答案
(1)
(2)S=
解析
(1)对于
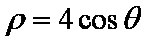
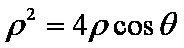
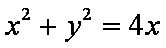
对于:由
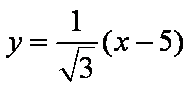
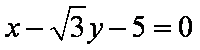
(2)由(1)可知
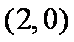
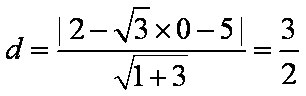
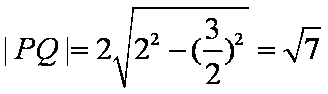
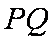

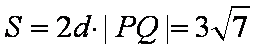
知识点
在直角坐标系







(1)求曲线

(2) 设




正确答案
见解析
解析
(1)由曲线

两式两边平方相加得:
即曲线
由曲线

即
即曲线

(2)由(1)知椭圆



所以当




知识点
在直角坐标系







(1)求曲线

(2)求曲线

正确答案
(1)C1:x2+(y-1)2=1,C2:x-y+1=0
(2)1
解析
(1)将


将

(2) 由(1)知曲线






知识点
已知直线



(1)求直线

(2)求直线

正确答案
见解析
解析
解析:(1)把直线

把曲线

∴其直角坐标方程为
(2)由(1)知曲线
∴圆心到直线的距离

知识点
已知曲线





(1)化曲线
(2)若直线



正确答案
(1)y2=4x(2)8
解析
(1)对于曲线


把互化公式


(可验证原点
(2)根据条件直线



由


令


所以
知识点
扫码查看完整答案与解析