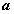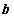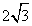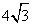平面向量数量积坐标表示的应用
共7题

· 平面向量数量积坐标表示的应用

平面向量数量积坐标表示的应用
共7题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

4．已知向量（2，3），（-1，2），若与共线，则（）

D-2

正确答案

解析

考查方向

本题考查向量的坐标运算法则、考查向量共线的坐标形式的充要条件．

解题思路

利用向量的坐标运算求出两个向量的坐标；利用向量共线的充要条件列出方程求出m的值。

易错点

共线与垂直的条件，出现混淆。

知识点

平面向量数量积坐标表示的应用

题型：简答题

简答题 · 16 分

在平面直角坐标系xOy中，已知椭圆+=1（a＞b＞0）过点（1，1）。

（1）若椭圆的离心率为，求椭圆的方程；

（2）若椭圆上两动点P，Q，满足OP⊥OQ。

①已知命题：“直线PQ恒与定圆C相切”是真命题，试直接写出圆C的方程；（不需要解答过程）

②设①中的圆C交y轴的负半轴于M点，二次函数y=x2﹣m的图象过点M，点A，B在该图象上，当A，O，B三点共线时，求△MAB的面积S的最小值。

正确答案

见解析。

解析

（1）由e=，

则a：b：c=：1：1；

∴可设椭圆方程为+=1，将（1，1）代入得

+=1，

∴b2=，a2=3，

∴椭圆方程为+=1；

（2）①根据题意，用特殊值来验证，如图所示；

∵椭圆过点（1，1），

∴+=1，

即a2+b2=a2b2；

又OP⊥OQ，

∴|PQ|=；

∴点O到直线PQ的距离|OM|==1；

∴根据椭圆的对称性，得出圆C的方程是x2+y2=1；

②由题意，二次函数为y=x2﹣1，

设直线AB的方程为y=kx，

由，消去y得，x2﹣kx﹣1=0；

设A（x1，y1），B（x2，y2），则x1+x2=k，x1x2=﹣1，

则S=OM•|x1﹣x2|==；

当k=0时，△MAB的面积S的最小值为1。

知识点

平面向量数量积坐标表示的应用

题型：单选题

单选题 · 5 分

已知两不共线向量，，则下列说法不正确的是

B与的夹角等于

D与在方向上的投影相等

正确答案

解析

略

知识点

平面向量数量积的运算数量积表示两个向量的夹角数量积判断两个平面向量的垂直关系平面向量数量积坐标表示的应用

题型：单选题

单选题 · 5 分

设是两条不同的直线，是两个不同的平面。下列四个命题正确的是（）

正确答案

解析

略

知识点

平面向量数量积坐标表示的应用

题型：简答题

简答题 · 12 分

已知△ABC的内角A，B，C的对边分别为a，b，c，满足。

（1）求角C

（2）若向量与共线，且c=3，求a、b的值。

正确答案

见解析。

解析

（1）∵，

∴，化为，

∴，

∵C∈（0，π），∴，

∴，解得C=。

（2）∵向量与共线，∴sinB﹣2sinA=0，

由正弦定理得，∴b=2a。

由余弦定理得c2=a2+b2﹣2absinC，

∴，化为a2+b2﹣ab=9。

联立，解得。

知识点

平面向量数量积坐标表示的应用

题型：单选题

单选题 · 5 分

已知平面向量，，且，则实数的值为

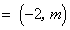
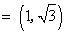
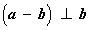
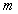
正确答案

解析

略

知识点

数量积判断两个平面向量的垂直关系平面向量数量积坐标表示的应用

题型：填空题

填空题 · 5 分

已知向量，若，则的值为（）.

正确答案

-1或3

解析

略

知识点

向量的线性运算性质及几何意义平面向量数量积的运算平面向量数量积坐标表示的应用

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 向量在几何中的应用

百度题库 > 高考 > 文科数学 > 平面向量数量积坐标表示的应用

扫码查看完整答案与解析