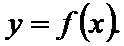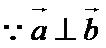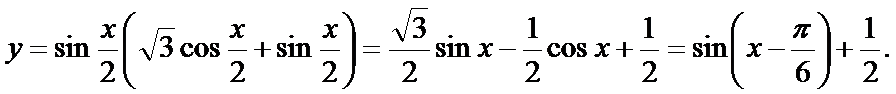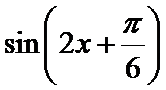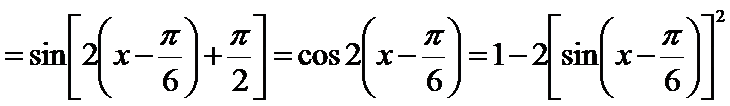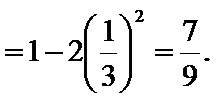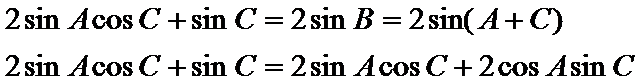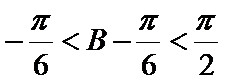- 三角形中的几何计算
- 共63题
16.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知
(1)求
(2)若
正确答案
(1)
解析
试题分析:(1)利用两角和的正切公式及同角三角函数关系式求解;(2)求出角A的正弦值和余弦值,利用正弦定理求出b,再利用诱导公式和两角和的正弦求出sinC,最后求三角形的面积
(1)由


所以

(2)由

又由


由sinC=sin(A+B)=

设△ABC的面积为S,则
考查方向
解题思路
(1)由两角和与差的正切函数公式及已知可得tanA,由倍角公式及同角三角函数关系式即可得解.
(2)由

易错点
同角三角函数关系,诱导公式的应用.
知识点
已知A、B、C为△ABC的内角,tanA、tanB是关于方程x2+
23.求C的大小
24.若AB=1,AC=
正确答案
C=60°
解析
由已知,方程x2+
△=(
所以p≤-2或p≥
由韦达定理,有tanA+tanB=-
于是1-tanAtanB=1-(1-p)=p≠0
从而tan(A+B)=
所以tanC=-tan(A+B)=
所以C=60°
考查方向
解题思路
1.第(1)问先求出p的范围,然后根据韦达定理和两角和的正切公式求出角C的大小;
易错点
1.不会利用韦达定理导出p和角A,B的关系;
正确答案
p=-1-
解析
(II)由正弦定理,得
sinB=
解得B=45°或B=135°(舍去)
于是A=180°-B-C=75°
则tanA=tan75°=tan(45°+30°)=
所以p=-



考查方向
解题思路
.第(2)问由正弦定理先求出角B,A,后即可求出p的值。
易错点
没有注意p的取值范围导致出错。
17.在



(1)求角



正确答案
(1)
解析
试题分析:本题属简单的三角恒定变换和解三角形的问题,(1)先由正弦定理将边的关系转化为角的关系然后化简之后可以求出角B;(2)利用余弦定理以及已知条件即可解出三角形的面积。
试题解析:(1)∵

∴
∵

∵

∵


(2)将



即
∴

于是, 
考查方向
解题思路
本题考查了简单的三角恒定变换和解三角形的问题,解题步骤如下:(1)先由正弦定理将边的关系转化为角的关系然后化简之后可以求出角B;(2)利用余弦定理以及已知条件即可解出三角形的面积。
易错点
一般是容易出现计算失误。
知识点
16. 已知函
(I)求函数
(II)在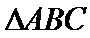


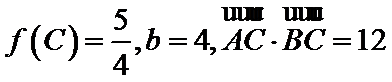
正确答案
见解析
解析
考查方向
解题思路
该题解题思路如下
1)使用和角公式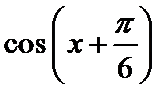
2)利用倍角公式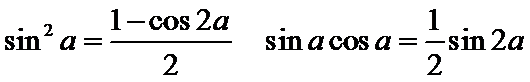
3)使用辅助角公式对解析式化简
4)利用特殊角的三角函数求值得到角C,
5)使用余弦定理得到a,b的关系,使用余弦定理求c
易错点
该题易于忽略了对C的范围的判断,该题属于简单
知识点
已知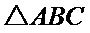
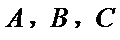
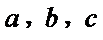
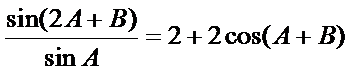
17.求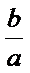
18.若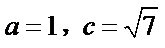
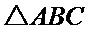
正确答案
(1)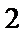
解析
(Ⅰ)∵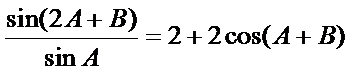
∴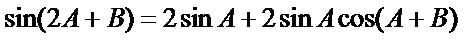
∴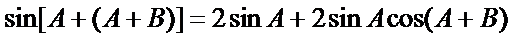
∴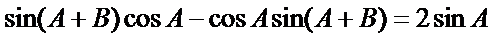
∴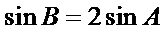
∴
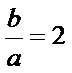
考查方向
解题思路
1)第一问中用两角和差公式和三角恒等变换化简得到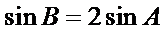
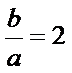
2)第二问中用倍余弦定理得到一个角,在用三角形面积公式求得面积。
易错点
1)第一问中想不到将角
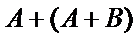
2)第二问中用余弦定理求角时容易将特殊角记错。
正确答案
(2)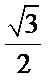
解析
(Ⅱ)∵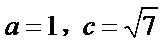
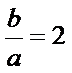
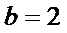
∴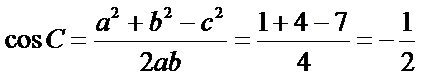
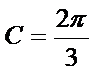
∴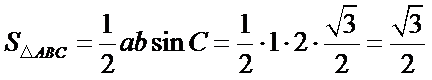
即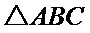
考查方向
解题思路
1)第一问中用两角和差公式和三角恒等变换化简得到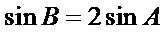
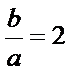
2)第二问中用倍余弦定理得到一个角,在用三角形面积公式求得面积。
易错点
1)第一问中想不到将角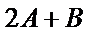
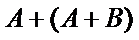
2)第二问中用余弦定理求角时容易将特殊角记错。
13.设


正确答案
4
解析
由





正弦定理与余弦定理.
考查方向
解题思路
本题考查正弦定理与余弦定理的应用,先由正弦定理将
易错点
注意运算的准确性及最后结果还需开方.
知识点
13.设△




正确答案

解析
由








考查方向
解题思路
1.先根据正弦定理将角间的关系转化为边
易错点
不会将题中的条件
知识点
已知向量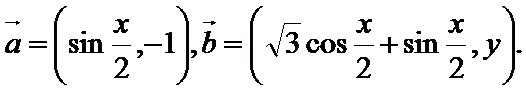
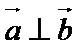
17.若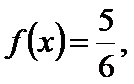
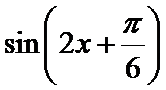
18.在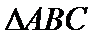
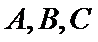
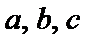
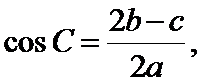
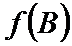
正确答案
解析
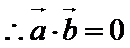
得
即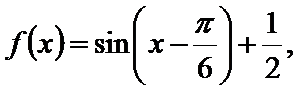
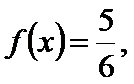
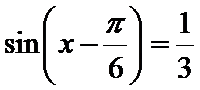
考查方向
解题思路
先通过向量垂直,得到三角关系,利用辅助角公式得到三角函数的解析式y=sin(x-
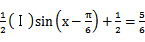
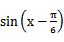

易错点
向量的坐标运算,三角函数的恒等变换
正确答案
(0,
解析
由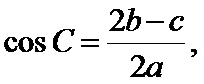
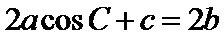
∴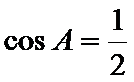

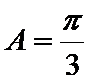
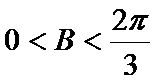
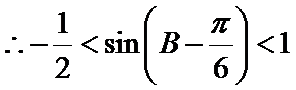
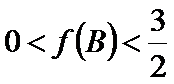
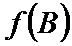
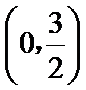
考查方向
解题思路
将边用正弦定理进行转化,得到cosA=


易错点
向量的坐标运算,三角函数的恒等变换
已知向量

17.若

18.在




正确答案
解析

得
即


考查方向
解题思路
先通过向量垂直,得到三角关系,利用辅助角公式得到三角函数的解析式y=sin(x-



易错点
向量的坐标运算,三角函数的恒等变换
正确答案
(0,
解析
由

∴







考查方向
解题思路
将边用正弦定理进行转化,得到cosA=


易错点
向量的坐标运算,三角函数的恒等变换
5.设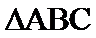
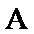
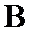
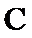
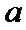
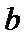
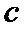
若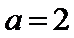
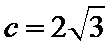
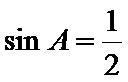

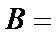
正确答案
解析
由题意可知,由正弦定理可得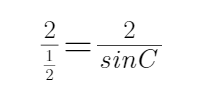
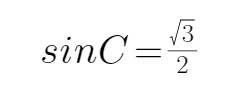
而A=30度,当C=60度时,B=90度,不符合b<c
当C=120度,B=30度,符合,所以选A
考查方向
正弦定理的性质和应用
解题思路
利用正弦定理求出角C的大小,然后求角B的大小
易错点
正弦定理公式记忆混淆
知识点
扫码查看完整答案与解析