- 圆与圆的位置关系及其判定
- 共31题
16.已知







(Ⅰ)求
(Ⅱ)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数集





(1)分别判断数集


(2)求


(3)由(2)及通过对

正确答案
(1)由于



由于








(2)∵




从而
当




从而



故数列
(3)命题一:对于一切大于或等于3的奇数


证明:由(2),不妨设





因为







第1组:

第2组:

第3组:

第


上一组的第2项总大于下一组的第1项,再注意到
第1组的各数从左到右依次为:
第2组的各数从左到右依次为:
第3组的各数从左到右依次为:
第

于是,有
由(﹡),




成等比数列.
命题二:对于一切大于或等于6的偶数


证略(同命题一的证明类似)
命题三:对于一切





(证略)若学生指出:当


例如数列

解析
解析已在路上飞奔,马上就到!
知识点
11.已知向量



正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
5. 若圆C1:x2+y2=1与圆C2:x2+y2-6x-8y+m=0外切,则m=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
在圆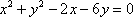

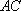
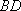
正确答案
解析
略。
知识点
已知圆




正确答案
解析
略
知识点
平面直角坐标系中,O为坐标原点,给定两点A(1,0),B(0,一2),点C满足


(1)求点C的轨迹方程;
(2)设点C的轨迹与椭圆

(3)在(2)的条件下,若椭圆的离心率不大于
正确答案
见解析
解析
解析:(1)设

有

(2)由
设
则
∵以MN为直径的圆过原点O,

(3)
∴椭圆长轴的取值范围是
知识点
2012年春节前,有超过20万名广西、四川等省籍的外来务工人员选择驾乘摩托车沿321国道长途跋涉返乡过年,为防止摩托车驾驶人因长途疲劳驾驶,手脚僵硬影响驾驶操作而引发交事故,肇庆市公安交警部门在321国道沿线设立了多个长途行驶摩托车驾乘人员休息站,让过往返乡过年的摩托车驾驶人有一个停车休息的场所。交警小李在某休息站连续5天对进站休息的驾驶人员每隔50辆摩托车,就进行省籍询问一次,询问结果如图4所示:
(1)问交警小李对进站休息的驾驶人员的省籍询问采用的是什么抽样方法?
(2)用分层抽样的方法对被询问了省籍的驾驶人员进行抽样,若广西籍的有5名,则四川籍的应抽取几名?
(3)在上述抽出的驾驶人员中任取2名,求至少有1名驾驶人员是广西籍的概率。
正确答案
见解析。
解析
(1)∵


∴
由正弦定理
(2)∵

又∵

∴
知识点
15.把正偶数依次按如下规律进行排序:第一个括号括一个数,第二个括号括两个数,第三个括号括三个数,第四个括号括一个数,…,依次循环,如(2),(4,6),(8,10,12),(14),…,则第50个括号内的各数的和为 .
正确答案
394
解析
由题意可知,每三个括号将用掉数列的6项,所以前49个括号共用了数列的97项,第50个括号里有两个数分别是196和198,故两个数的乘积为394.
知识点
16.与直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析