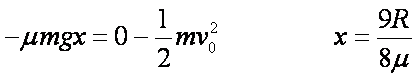- 生活中的圆周运动
- 共107题
如图,在竖直平面内有一固定光滑轨道,其中AB是长为R的水平直轨道,BCD是圆心为O、半径为R的
(1)小球从在AB段运动的加速度的大小;
(2)小球从D点运动到A点所用的时间。
正确答案
见解析。
解析
(1)小球在BCD段运动时,受到重力



设小球在C点的速度大小为

小球从B点运动到C点,机械能守恒,设B点处小球的速度大小为

由于小球在AB段由静止开始做匀加速运动,设加速度大小为

由②③④式得 
(2)设小球在D处的速度大小为



设从D点运动到A点所用时间为

由④⑤⑥⑦⑧式得

知识点
图18(a)所示的装置中,小物块A.B质量均为m,水平面上PQ段长为l,与物块间的动摩擦因数为μ,其余段光滑。初始时,挡板上的轻质弹簧处于原长;长为r的连杆位于图中虚线位置;A紧靠滑杆(A.B间距大于2r)。随后,连杆以角速度ω匀速转动,带动滑杆作水平运动,滑杆的速度-时间图像如图18(b)所示。A在滑杆推动下运动,并在脱离滑杆后与静止的B发生完全非弹性碰撞。
(1)求A脱离滑杆时的速度uo,及A与B碰撞过程的机械能损失ΔE。
(2)如果AB不能与弹簧相碰,设AB从P点到运动停止所用的时间为t1,求ω得取值范围,及t1与ω的关系式。
(3)如果AB能与弹簧相碰,但不能返回道P点左侧,设每次压缩弹簧过程中弹簧的最大弹性势能为Ep,求ω的取值范围,及Ep与ω的关系式(弹簧始终在弹性限度内)。
正确答案
见解析。
解析
(1)设连杆的水平位移为x 取水平向右的方向为正则:


V0=
AB相碰由动量守恒得:mv0=2mv ②
AB系统机械能损失ΔE=
由①②③得:

(2)AB在pq上做匀减速直线运动,加速度为:

s≤l ⑥
0=v+at1 ⑦
由④⑤⑥⑦得:

(3)AB从p开始到弹簧压缩到最短时过程由能量守恒得:
可得到:
设AB返回时刚好到达P点时速度为0,则此时角速度最大
全过程由能量守恒得:
解得:
知识点
如图所示,质量为m1=lkg的小物块由静止轻轻放在水平匀速运动的传送带上,从A点随传送带运动到水平部分的最右端B点,经半圆轨道C点沿圆弧切线进入竖直光滑的半圆轨道,恰能做圆周运动。C点在B点的正上方,D点为轨道的最低点。小物块m1到达D点后与静止在D点的质量为m2=0.5kg小物块发生碰撞,碰撞后,两者均做平抛运动,m2恰好垂直于倾斜挡板打在挡板跟水平面相交的E点,m1落在F点,已知半圆轨道的半径R=0.5m,D点距水平面的高度h =0.45m,倾斜挡板与水平面之间的夹角θ=53°,不考虑空气阻力,试求:(1)摩擦力对小物块m1做的功;(2)水平面上EG间的距离;(3)小物块m1碰撞m2后经过D点时对轨道压力的大小。(题目中可能要用到的数据:g=10 m/s2,sin37°=0.6,cos37°=0.8)
正确答案
见解析。
解析
(1)设小物体m1经过C点时的速度大小为v1,因为经过C点恰能做圆周运动,
由牛顿第二定律得:


小物体m1由A到B过程中,设摩擦力对小物体做的功为Wf,由动能定理得:

(2)小物体m2离开D点后做平抛运动,设经过时间t打在E点,由

设小物体m2打在E点时速度的水平、竖直分量分别为

速度跟竖直方向的夹角为θ,则:


解得:

(3)设小物体m1经过D时的速度大小为v2,对C点运动到D点的过程,
由机械能守恒定律得: 
小物体m1经过D点时,与m2发生碰撞,由动量守恒定律可得,

设轨道对m1的支持力大小为FN,由牛顿第二定律得:

代入数据,联立解得:FN=28N,(1分)由牛顿第三定律可知,
小物体m1对轨道的压力大小为:
知识点
14.(16分)一转动装置如图所示,四根轻杆OA、OC、AB和CB与两小球以及一小环通过铰链连接,轻杆长均为l,球和环的质量均为m,O端固定在竖直的轻质转轴上,套在转轴上的轻质弹簧连接在O与小环之间,原长为L,装置静止时,弹簧长为
(1)弹簧的劲度系数k;
(2)AB杆中弹力为零时,装置转动的角速度
(3)弹簧长度从

正确答案
(1)装置静止时,设





小环受到弹簧的弹力
小环受力平衡
小球受力平衡
解得
(2)设






小环受到弹簧的弹力
小环受力平衡 
对小球

解得
(3)弹簧长度为






小环受到弹簧的弹力
小环受力平衡
对小球
解得
整个过程弹簧弹性势能变化为零,则弹力做的功为零,由动能定理
解得
解析
解析已在路上飞奔,马上就到!
知识点
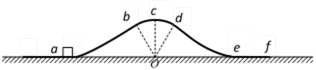
如图15所示,一条轨道固定在竖直平面内,粗糙的ab段水平,bcde段光滑,cde段是以O为圆心、R为半径的一小段圆弧。可视为质点的物块A和B紧靠在一起,静止于b处,A的质量是B的3倍。两物块在足够大的内力作用下突然分离,分别向左、右始终沿轨道运动。B到b点时速度沿水平方向,此时轨道对B的支持力大小等于B所受重力的3/4,A与ab段的动摩擦因数为μ,重力加速度g,求:
(1)物块B在d点的速度大小;
(2)物块A滑行的距离s
正确答案
(1)υ =

解析
(1)B在d点,根据牛顿第二定律有:
mg −
解得:υ =
(2)B从b到d过程,只有重力做功,机械能守恒有:



3mυA = mυB ②

联立①②③
s =
知识点
如图所示,质量M=2kg的滑块套在光滑的水平轨道上,质量m=1kg的小球通过长L=0.5m的轻质细杆与滑块上的光滑轴O连接,小球和轻杆可在竖直平面内绕O轴自由转动。开始轻杆处于水平状态。现给小球一个竖直向上的初速度v0=4m/s,g取10m/s2。
(1)若锁定滑块,试求小球通过最高点P时对轻杆的作用力大小和方向。
(2)若解除对滑块的锁定,试求小球通过最高点时的速度大小。
(3)在满足(2)的条件下,试求小球击中滑块右侧轨道位置点与小球起始位置点间的距离。
正确答案
见解析。
解析
(1)设小球能通过最高点,且此时的速度为v1。在上升过程中,因只有重力做功,小球的机械能守恒。则
设小球到达最高点时,轻杆对小球的作用力为F,方向向下,则F+mg=
联立解得F=2N,由牛顿第三定律可知,小球对轻杆的作用力大小为2N,方向竖直向上。
(2)解除锁定后,设小球通过最高点时的速度为v2,此时滑块的速度为V。在上升过程中,因系统在水平方向上不受外力作用,水平方向的动量守恒。以水平向右的方向为正方向,有
mv2+MV=0
在上升过程中,因只有重力做功,系统的机械能守恒,则

(3)设小球击中滑块右侧轨道的位置点与小球起始点的距离为s1,滑块向左移动的距离为s2,任意时刻小球的水平速度大小为v3,滑块的速度大小为V/。由系统水平方向的动量守恒,得
mv3-MV′=0,两边同乘以△t,得mv3△t-MV′△t=0,故对任意时刻附近的微小间隔△t都成立,累积相加后,有ms1-Ms2=0,又s1+s2=2L,得s1=
知识点
小明站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,甩动手腕,使球在竖直平面内做圆周运动。当球某次运动到最低点时,绳突然断掉,球飞行水平距离d后落地。如题24图所示。已知握绳的手离地面高度为d,手与球之间的绳长为
(1)求绳断时球的速度大小

(2)向绳能承受的最大拉力多大?
(3)改变绳长,使球重复上述运动,若绳仍在球运动到最低点时断掉,要使球抛出的水平距离最大,绳长应是多少?最大水平距离为多少?
正确答案
见解析
解析
(1)设绳断后球飞行时间为t,由平抛运动规律,有
竖直方向

得v1=
由机械能守恒定律,有


得 v2=
(2)设绳能承受的最大拉力大小为T,这也是球受到绳的最大拉力大小.
球做圆周运动的半径为R=
由圆周运动向心力公式,有T-mg=
得T=
(3)设绳长为l,绳断时球的速度大小为v3,绳承受的最大拉力不变,
有T-mg= 
绳断后球做平抛运动,竖直位移为d-l,水平位移为x,时间为t1.
有d-l= 
得x=4
当l=

知识点
图4是滑到压力测试的示意图,光滑圆弧轨道与光滑斜面相切,滑到底部B处安装一个压力传感器,其示数N表示该处所受压力的大小,某滑块从斜面上不同高度h处由静止下滑,通过B是,下列表述正确的有
正确答案
解析
设滑块在B点的速度大小为v,开始到B点由动能定理得: 

知识点
如图所示,水平面上固定一轨道,轨道所在平面与水平面垂直,其中bcd是一段以O为圆心、半径为R的圆弧,c为最高点,弯曲段abcde光滑,水平段ef粗糙,两部分平滑连接,a、O与ef在同一水平面上。可视为质点的物块静止于a点,某时刻给物块一个水平向右的初速度,物块沿轨道经过c点时,受到的支持力大小等于其重力的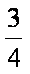
求:
(1)物块经过c点时速度v的大小;
(2)物块在a点出发时速度v0的大小;
(3)物块在水平部分ef上滑行的距离x。
正确答案
见解析。
解析
(1)在c点对物块受力分析,根据牛顿运动定律:
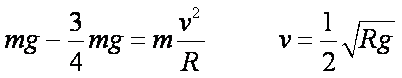
(2)物块A从a到c,根据机械能守恒定律:
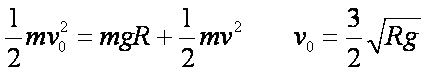
(3)设物块A在水平轨道上滑行的距离为x,从e到f,根据动能定理:
知识点
如图所示,将直径为2R的半圆形导轨固定在竖直面内的A、B两点,直径AB与竖直方向的夹角为60°。在导轨上套一质量为m的小圆环,原长为2R、劲度系数

(1)圆环的速率v;
(2)导轨对圆环的作用力F的大小?
正确答案
解:
(1)由几何知识得,圆环在C点、D点时,弹性绳形变量相同,弹性势能相等。由机械能守恒定律,有
由几何关系可知 
解得 
(2)圆环在D点受力如图,弹性绳的弹力

其中
由牛顿第二定律,有

解得
解析
略
知识点
扫码查看完整答案与解析