- 生活中的圆周运动
- 共107题
如图所示，光滑的水平轨道AB与半径为R的光滑的半圆形轨道BCD相切于B点，水平轨道AB部分存在水平向右的匀强电场E，半圆形轨道处于竖直平面内，B为最低点，D为最高点．一质量为m、带正电的小球从距B点x的位置在电场力的作用下由静止开始沿AB向右运动，并能恰好通过最高点D，则下列物理量的变化对应关系正确的是
正确答案
解析
略
知识点
如图所示，足够长的斜面倾角θ=30°，斜面底端A点与一半径为R的光滑半圆轨道平滑连接，半圆轨道的直径与地面垂直。已知小物体与斜面间的动摩擦因数为μ=
（1）若小物体在斜面上从与圆心O等高的位置由静止释放，则小物体第一次滑到A点所用的时间为多少？
（2）在（1）的情况下，小物体在斜面上滑行的总路程为多少？
（3）要使小物体能通过圆轨道最高点B，求小物体在斜面上由静止释放的高度。
正确答案
（1）
（2）4R
（3）2.5R
解析
（1）物块沿斜面下滑过程中，在重力、支持力和摩擦力作用下做匀加速运动，设下滑加速度为a，到达斜面底端B时的时间为t，则：
mgsinθ﹣μmgcosθ=ma
则得：a=g（sinθ﹣μcosθ）=10×（sin30°﹣
物体的位移：
由
得：t=
（2）由题意可知，最后物块的机械能全部转化为内能，由功能关系得：μmgcosθS=mgR
整理得：S=4R
（3）要使小物体能通过圆轨道最高点B，在物体在最高点的向心力要大于等于重力，即：
从释放到到达B的过程中，由机械能守恒得：
联立以上方程得：h=2.5R
知识点
AB是竖直平面内的四分之一光滑圆弧形轨道，圆轨道半径R=1.25m，如图所示。一质量 m = 1 kg的小球自A点起由静止开始沿轨道下滑至 B点水平抛出，落在地上的C点，B 点距离地面高度 h = 0.8 m．重力加速度 g 取10 m/s2。。
求
（1）小球从B点抛出时的速度大小；
（2）小球在圆弧轨道底端B点受到的支持力大小；
（3）小球落地点C距离抛出点B的水平距离x。
正确答案
见解析。
解析
（1）小球从A到B，根据机械能守恒定律
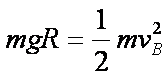
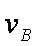
（2）由牛顿第二定律知：FN - mg = m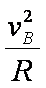
解得：FN = 30 N
（3）物块从B点到C点做平抛运动
由h =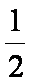 
和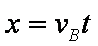
解得x=2m
知识点
如图一个滑块质量为m从半径为R的半圆形截面的凹槽顶点A处由静止滑下，滑过最低点B后又在另一侧上滑至最高点C恰能静止下来，C点与圆心边线与水平方向成θ角，设滑都必须块与凹槽的动摩擦因数为μ，最大静摩擦力约等于滑动摩擦力，则下述分析正确的有（ ）
A滑块在C点静止时受到的静摩擦力是
B滑块在C点静止时对凹面的压力是
C滑块由B向C运动中摩擦阻力越来越大
D由A到C滑块克服摩擦力做功
正确答案
解析
略
知识点
如图所示，在竖直平面内有一固定轨道，其中AB是长为R的粗糙水平直轨道，BCD是圆心为O、半径为R的3/4光滑圆弧轨道，两轨道相切于B点．在推力作用下，质量为m的小滑块从A点由静止开始做匀加速直线运动，到达B点时即撤去推力，小滑块恰好能沿圆轨道经过最高点C。重力加速度大小为g，取AB所在的水平面为零势能面。则小滑块
正确答案
解析
略
知识点
扫码查看完整答案与解析