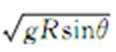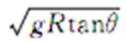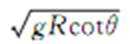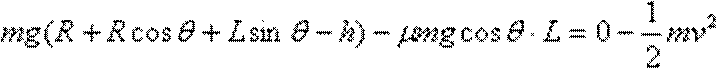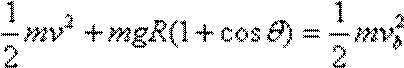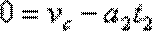- 生活中的圆周运动
- 共107题
2.如图所示,斜轨道与半径为R的半圆轨道平滑连接,点A与半圆轨道最高点C等高,B为轨道的最低点(滑块经B点无机械能损失).现让小滑块(可视为质点)从A点开始以速度v0沿斜面向下运动,不计一切摩擦,关于滑块运动情况的分析,正确的是( )
正确答案
解析
每小题给出的选项中,有的只有一个选项正确,有的有多个选项正确,全部选对的得3分,选对但不全的得2分,有选错的得0分
知识点
14.如图所示,半径为R的竖直光滑圆轨道内侧底部静止放着一个光滑小球。现给小球一个撞击使其在瞬间得到一个水平初速度v0,若v0大小改变,则小球能够上升的最大高度(距离底部)也随之改变,则下列说法中正确的是( )
正确答案
解析
在每小题给出的四个选项中,有一个选项或多个选项正确。全部选对的得3分,选不全的得2分,有选错或不答的得0分。
知识点
16.如图所示,半径R=0.9m的四分之一圆弧形光滑轨道竖直放置,圆弧最低点B与长为L=1m的水平面相切于B点,BC离地面高h=0.45m,C点与一倾角为

(1)小滑块刚到达圆弧的B点时对圆弧的压力:
(2)小滑块到达C点时速度的大小:
(3)小滑块从C点运动到地面所需的时间.
正确答案
(1)设滑块到B点速度为VB,由机械能守恒
在B点:
得 N=3mg=30N
由牛顿第三定律,滑块在B点对圆弧的压力大小为30N
(2)由动能定理,
(3)滑块离开C点后做平抛运动,设其下落h的时间为t,则
由
得t=0.3s
t=0.3s内滑块的水平位移x=vct=1.2m
而斜面的水平长度

所以小滑块从C点运动到地面所需的时间为0.3s
解析
解析已在路上飞奔,马上就到!
知识点
14.如图所示,竖直平面内的一半径R=0.50m的光滑圆弧槽BCD,B点与圆心O等高,一水平面与圆弧槽相接于D点.质量m=0.10kg的小球从B点正上方H=0.95m高处的A点自由下落,由B点进入圆弧轨道,从D点飞出后落在水平面上的Q点,DQ间的距离s=2.4m,球从D点飞出后的运动过程中相对水平面上升的最大高度h=0.80m,取g=10m/s2,不计空气阻力,求:
(1)小球经过最低点C时小球对轨道的压力大小N;
(2)小球经过最高点P的速度大小vP;
(3)D点与圆心O的高度差hOD
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.山城重庆的轻轨交通颇有山城特色,由于地域限制,弯道半径很小,在某些弯道上行驶时列车的车身严重倾斜。每到这样的弯道乘客都有一种坐过山车的感觉,很是惊险刺激。假设某弯道铁轨是圆弧的一部分,转弯半径为R,重力加速度为g,列车转弯过程中倾角(车身与水平面夹角)为θ,则列车在这样的轨道上转弯行驶的安全速度(轨道不受侧向挤压)为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如图,一质量为M的光滑大圆环,用一细轻杆固定在竖直平面内;套在大环上质量为m的小环(可视为质点),从大环的最高处由静止滑下.重力加速度大小为g.当小环滑到大环的最低点时,大环对轻杆拉力的大小为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.如图所示,水平桌面上有一轻弹簧,左端固定在A点,自然状态时其右端位于B点。水平桌面右侧有一竖直放置的光滑轨道MNP,其形状为半径R=0.8m的圆环剪去了左上角135°的圆弧,MN为其竖直直径,P点到桌面的竖直距离也是R。用质量ml=0.4kg的物块将弹簧缓慢压缩到C点,释放后弹簧恢复原长时物块恰停止在B点。用同种材料、质量为m2=0.2kg的物块将弹簧缓慢压缩到C点释放,物块过B点后做匀变速运动,其位移与时间的关系为s=6t-2t2,物块飞离桌面后由P点沿切线落入圆轨道。不计空气阻力g=l0m/s2
求:
(1)物块m2过B点时的瞬时速度Vo及与桌面间的滑动摩擦因数;
(2)BP向的水平距离;
(3)判断m2能否沿圆轨道到达M点(要有计算过程);
(4)释放后m2运动过程中克服摩擦力做的功。
正确答案
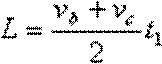
(2)s=4.1m
(3)
(4)
解析
解析已在路上飞奔,马上就到!
知识点
23.光滑圆轨道和两倾斜直轨道组成如图所示装置,其中直轨道bc粗糙,直轨道cd光滑,两轨道相接处为一很小的圆弧。质量为m=0.1kg的滑块(可视为质点)在圆轨道上做圆周运动,到达轨道最高点a时的速度大小为v=--4m/s,当滑块运动到圆轨道与直轨道bc的相切处6时,脱离圆轨道开始沿倾斜直轨道bc滑行,到达轨道cd上的.d点时速度为零。若滑块变换轨道瞬间的能量损失可忽略不计,已知圆轨道的半径为R=0.25m,直轨道bc的倾角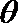
(1)滑块在圆轨道最高点a时对轨道的压力大小;
(2)滑块与直轨道bc之间的动摩擦因数;
(3)滑块在直轨道bc上能够运动的时间。
正确答案
(1)在圆轨道最高点a处对滑块由牛顿第二定律得:
∴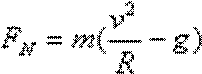
由牛顿第三定律得滑块在圆轨道最高点a时对轨道的压力大小为5.4N
(2)从a点到d点全程由动能定理得:
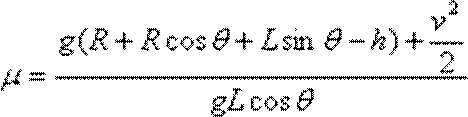
(3)设滑块在bc上向下滑动的加速度为a1,时间为t1,向上滑动的加速度为a2,时间为t2;在c点时的速度为vc。
由c到d:
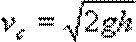
a点到b点的过程:
∴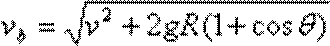
在轨道bc上:
下滑:

上滑:


∵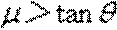
滑块在两个斜面上运动的总时间:
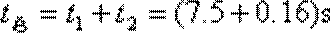
解析
解析已在路上飞奔,马上就到!
知识点
22.在竖直平面内有一个粗糙的
求:
(1)小滑块离开轨道时的速度大小;
(2)小滑块运动到轨道最低点时,对轨道的压力大小;
(3)小滑块在轨道上运动的过程中,克服摩擦力所做的功。
正确答案
解:(1)小滑块离开轨道后做平抛运动,设运动时间为t,初速度为v,则

解得:
(2)小滑块到达轨道最低点时,受重力和轨道对它的弹力为N
根据牛顿第二定律:
解得:
根据牛顿第三定律,轨道受到的压力大小
(3)在滑块从轨道的最高点到最低点的过程中,根据动能定理:
所以小滑块克服摩擦力做功为0.2J。
解析
解析已在路上飞奔,马上就到!
知识点
24.如图所示,粗糙的斜面















(1)物体







(3)物体


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析