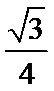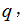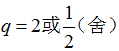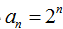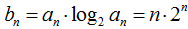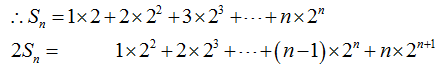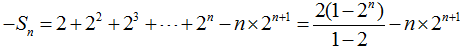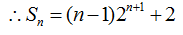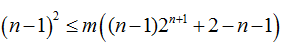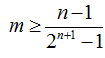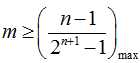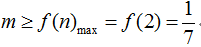- 数列与不等式的综合
- 共81题
等差数列{
(I)求{
(II)设


正确答案
(Ⅰ)设数列


所以

(Ⅱ)由(Ⅰ)知
当n=1,2,3时,
当n=4,5时,
当n=6,7,8时,
当n=9,10时,
所以数列

知识点
某公司为激励创新,计划逐年加大研发奖金投入。若该公司2015年全年投入研发奖金130万元,在此基础上,每年投入的研发奖金比上一年增长12%,则该公司全年投入的研发奖金开始超过200万元的年份是(参考数据:lg1.12=0.05,lg1.3=0.11,lg2=0.30) ( )
正确答案
知识点
19. 已知单调递增的等比数列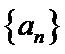
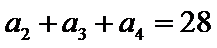
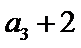
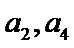
(I)求数列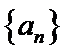
(II)设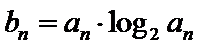
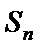
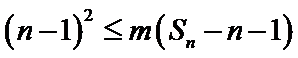
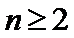
正确答案
(1)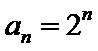
(2)
解析
试题分析:本题属于数列应用中的基本问题,题目的难度是逐渐由易到难,直接按照步骤来求
(Ⅰ)设等比数列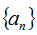
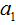
由题意可知: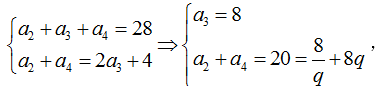
∴
所以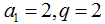
(Ⅱ)令
相减得
若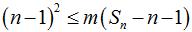
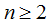
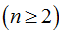
令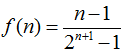
考查方向
解题思路
本题考查数列的性质,解题步骤如下:
1、利用基本量法求出通项;
2、利用错位相减法求和,恒成立问题转为最值问题
易错点
第一问中的辅助角容易计算错误
知识点
17.(本小题满分12分) 已知数列




(I) 求证:数列
(II) 证明:当

正确答案
(1)见解析;(2)见解析。
解析
试题分析:本题属于等差数列以及等差数列的性质,数列的通项公式和前n项和的关系,(1)根据题意直接利用通项公式和前n项和的关系来证明;(2)利用放缩法来证明。
考查方向
解题思路
本题考查等差数列以及等差数列的性质,数列的通项公式和前n项和的关系,解题步骤如下:(1)根据题意直接利用通项公式和前n项和的关系来证明;(2)利用放缩法来证明。
易错点
找不到通项公式和前n项和的关系。
知识点
15. 等差数列




(Ⅰ)求
(Ⅱ)求满足不等式

正确答案
(Ⅰ)
(Ⅱ)
解析
(Ⅰ)设数列

因为

因为


所以
(Ⅱ)因为


所以

解得


考查方向
本题考查了等差数列的通项公式、前n项和公式.在近几年的各省高考题出现的频率非常高.
解题思路
(Ⅰ)将通项公式代入
(Ⅱ)代入求和公式,解不等式即可.
易错点
移项时注意变号.
知识点
扫码查看完整答案与解析