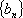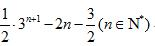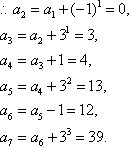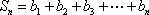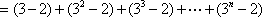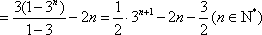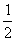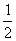- 等差数列与等比数列的综合
- 共63题
1
题型:填空题
|
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
1
题型:简答题
|
已知数列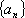
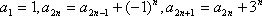
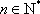
(1)求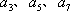
(2)求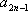

(3)记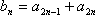
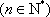

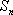
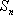

正确答案
(1)3,13,39(2)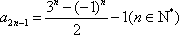
解析
(1)
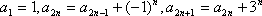
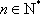
(2)由题知,有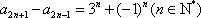
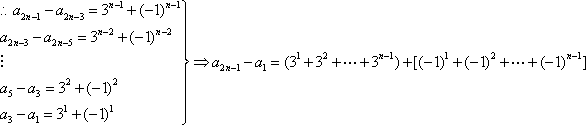
∴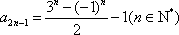
(3)由(2)可知,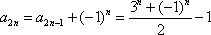
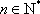
∴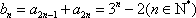
∴
知识点
等差数列与等比数列的综合
1
题型:简答题
|
在等差数列




(1)求数列
(2)设


正确答案
见解析。
解析
(1)由题意知:









(2)由 (1)知:
①当n为偶数时:
②当n为奇数时:
综上:
知识点
等差数列与等比数列的综合
1
题型:
单选题
|
设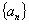
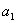
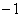
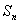
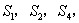
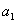
正确答案
D
解析
依题意得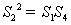
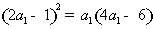
知识点
等差数列与等比数列的综合
1
题型:简答题
|
已知等差数列



(1)若

(2)若

正确答案
(1)

(2)
解析
本小题主要考查等比等差数列、等比数列和不等式等基础知识,考查运算求解能力,考查函数与方程思想、化归与转化思想。
(1)因为数列


所以
即


(2)因为数列


所以
即
知识点
数列与不等式的综合等差数列与等比数列的综合
下一知识点 : 数列与三角函数的综合
扫码查看完整答案与解析