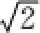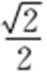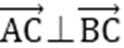平面向量数量积的运算
共232题

· 平面向量数量积的运算

平面向量数量积的运算
共232题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

6.已知向量a，b，c满足=a•b=2，(a-c)•(b-2c)=0，则的最小值为（）

正确答案

解析

由=a·b=2可知a，b的夹角为60°

不妨设a=(2，0)，b=(1，)，c=(x，y).

由(a-c)·(b-2c)=0可得(2-x)(1-2x)+(-y)( -2y)=0

整理得2x2-5x+2y2-y+2=0，即(x- )2+(y-)2=

则= 的最小值为-= .

知识点

向量的模平面向量数量积的运算

题型：单选题

单选题 · 5 分

2.已知椭圆C: 的左、右焦点分别为F1、F2，椭圆C上点A满足AF2⊥F1F2。若点P是椭圆C上的动点，则的最大值为（）

正确答案

解析

设的夹角为θ.

由条件知|AF2|为椭圆通径的一半，即|AF2|=，

则

于是要取得最大值，只需在上的投影值最大，

易知此时点P在椭圆短轴的上顶点

所以=cosθ≤，故选B.

知识点

平面向量数量积的运算椭圆的几何性质

题型：单选题

单选题 · 5 分

5.已知a，b是平面内两个互相垂直的单位向量，若向量c满足(a-c)·(b-c)=0，则|c|的最大值是（）

正确答案

解析

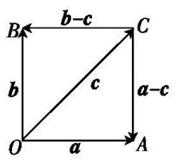
因为(a-c)·(b-c)=0，所以(a-c)⊥(b-c).

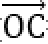
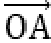
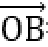
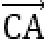
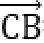
如图所示，设=c，=a，=b，=a-c，=b-c，即

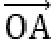
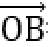
又⊥，所以O，A，C，B四点共圆.

当且仅当OC为圆的直径时，|c|最大，且最大值为.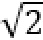

知识点

向量的模零向量平面向量数量积的运算

题型：单选题

单选题 · 5 分

1.已知ω>0,|φ|< ,函数f(x)=sin(ωx+φ)的部分图象如图所示。则=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由y=Asin（ωx+φ）的部分图象确定其解析式平面向量数量积的运算

题型：填空题

填空题 · 5 分

9.已知矩形ABCD的边长AB=2，BC=1，点E是AB边上的动点，则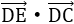的取值范围是_______。

正确答案

[0，4]

解析

如图所示，以AB，AD所在的直线分别为x轴，y轴建立平面直角坐标系xAy

由于AB=2，BC=1，故B(2，0)，C(2，1)，D(0，1).

因为E在AB边上，所以可设E(t，0)(0≤t≤2).

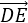
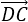
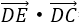
则=(t，-1)，=(2，0)，所以=2t，

又0≤t≤2，则0≤2t≤4

所以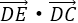的取值范围是[0，4].

知识点

平面向量数量积的运算向量在几何中的应用

继续学习学习下一知识点

下一知识点 : 数量积表示两个向量的夹角

百度题库 > 高考 > 文科数学 > 平面向量数量积的运算

扫码查看完整答案与解析