- 平面向量数量积的运算
- 共232题
13.已知平面向量





正确答案
解析
分三种情况考虑:
(1)


(1)


(1)


三者比较大小后知应选
知识点
16.已知向量α,β是平面内两个互相垂直的单位向量,若(5α-2γ)·(12β-2γ)=0,则|γ|的最大值是____________.
正确答案
解析
由题可知,(5α-2γ)·(12β-2γ)=4γ2-2γ(α+12β)=0,则γ2≤(
考查方向
本题主要考查了平面向量的垂直关系。
解题思路
解题步骤如下:利用公式求解。
易错点
本题要注意单位向量。
知识点
13. 已知



正确答案
解析
因为向量b与向量c平行,
所以s=(-1)*2=-2.
所以
所以答案为
考查方向
解题思路
先根据向量平行求解出s的值,进而求出余弦值
易错点
向量平行的计算
知识点
14.已知向量a,b满足a·(a-b)=2,且|a|=1,|b|=2,则a与b的夹角等于 .
正确答案
解析
设向量


所以
而|a|=1,|b|=2,所以
所以
又

考查方向
解题思路
1.先将a·(a-b)=2展开表示成
2.将|a|=1,|b|=2带入上式,得到
易错点
1.两个向量夹角的取值范围不清楚导致出错;2.数量积公式不会。
知识点
14.已知向量a=(1,

正确答案
2
解析
根据a=(1,

所以
即
考查方向
解题思路
本题考查平面向量的有关问题,
解题步骤如下:根据向量的坐标表示写出

易错点
1、向量模的求解出错;
2、向量的数量积的定义理解出错。
知识点
14.在直角梯形中










正确答案
5
解析
由题可知,以A为原点建系,

F(1/λ,√3),所以
考查方向
解题思路
1、画出平面图形并利用坐标系分析;2、表示平面向量,即可得到结果。
易错点
本题易在表示平面向量时发生错误。
知识点
10. 在边长为2的正三角形ABC中,D为BC中点,点P是该等边三角形的三边上的动点,求
正确答案
解析
设AD的中点为O,那么

考查方向
解题思路
本题可以建立坐标系用向量建立函数关系,可以直接用向量点积的几何意义建立函数关系求解
易错点
容易选择D答案,选择两个端点检验。
知识点
4.设向量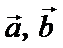
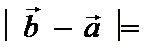
正确答案
解析

考查方向
解题思路
先使用向量减法的几何意义做
易错点
没理解向量模的 意义
知识点
12. 已知向量



正确答案
解析
考查方向
解题思路
本题主要是突破点在于垂直与数量积之间的转换
易错点
本题注意向量垂直与数量积之间的转换
知识点
16.已知





正确答案
10
解析
考查方向
本题主要考查了解三角形和平面向量及不等式
解题思路
本题考查解三角形和平面向量及不等式,解题思路如下:(1)利用公式表示数量积;
(2)利用不等式求解。
易错点
本题必须注意数量积公式
知识点
扫码查看完整答案与解析