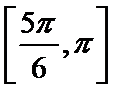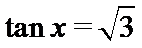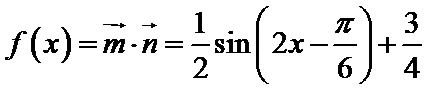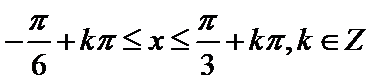- 平面向量数量积的运算
- 共232题
1
题型:简答题
|
17.已知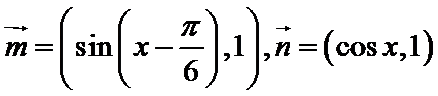
(1)若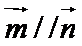
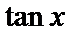
(2)若函数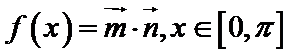
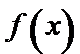
正确答案
(1)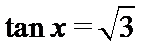
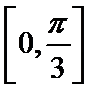
解析
试题分析:本题属于向量结合三角函数的问题,题目的难度是逐渐由易到难,
(1)直向量共线的坐标表示可以解出,
(2)先将函数求出来再化简最终可以得到单调增区间。
(1)由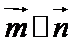
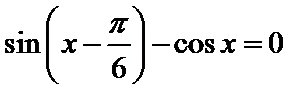
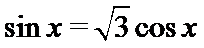
即
(2)
由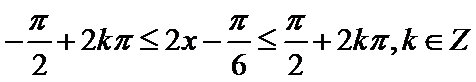
又因为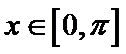
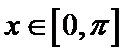
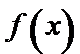
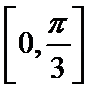
考查方向
本题考查了向量与三角函数以及函数综合考查。
解题思路
本题考查向量和三角函数的综合应用,解题步骤如下:由向量共线的坐标表示可以解出第一问,第二问先将函数求出来再化简最终可以得到单调增区间。
易错点
不知道怎么化简。
知识点
三角函数中的恒等变换应用平面向量数量积的运算
1
题型:
单选题
|
4.向量


正确答案
B
解析
由










考查方向
本题主要考查向量的数量积的运算和向量的夹角等知识,意在考查考生的运算求解能力。
解题思路
先根据题意得到

易错点
不会根据

知识点
平面向量数量积的运算数量积表示两个向量的夹角数量积判断两个平面向量的垂直关系
1
题型:填空题
|
14.已知|






正确答案
解析
因为

考查方向
数量积表示两个向量的夹角;平面向量数量积的运算
解题思路
先根据向量的数量积的定义,再根据向量垂直的性质求λ的值
易错点
平面向量及其应用
知识点
平面向量数量积的运算数量积判断两个平面向量的垂直关系
1
题型:填空题
|
13.已知




正确答案

解析
试题分析:根据向量数量积的定义求出向量的夹角,再利用题中给出的条件求出
∵











故答案为:
考查方向
本题考查了平面向量的运算、数量积的定义及性质、几何图形的应用,属于基础题.
解题思路
根据数量积得出

易错点
向量数量积的公式的应用.
知识点
向量的模平面向量数量积的运算
1
题型:
单选题
|
7.已知非零向量


正确答案
C
解析
由已知可得





考查方向
本题考查了向量垂直的性质运用以及利用向量的数量积求向量的夹角;熟练运用公式是关键..
解题思路
本题考查向量的数量积运算与向量夹角之间的关系,采用两向量垂直时其数量积为零来进行转化.本题属于基础题.
易错点
注意运算的准确性
知识点
向量的模平面向量数量积的运算
下一知识点 : 数量积表示两个向量的夹角
扫码查看完整答案与解析