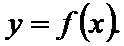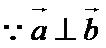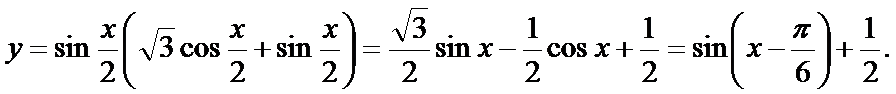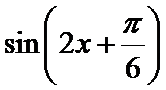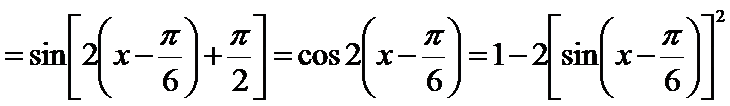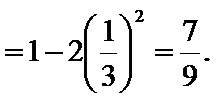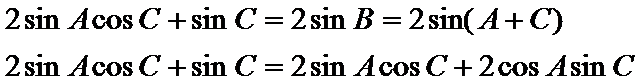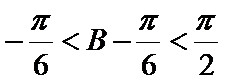- 平面向量数量积的运算
- 共232题
11.已知 







正确答案
解析
【解析】由








考查方向
解题思路
可以将其中一个向量的模设出来,其他 的用所设的表示出来,最后利用向量的数量积定义的变形式即可解出来。
易错点
不会利用数量积来求解。
知识点
15.在正方形





正确答案
[4,8-2
解析
设CN=x,CM=y,

因为

















考查方向
解题思路
画出正方形,设CN=x,CM=y,将

易错点
处理变量之间的整体关系及转化
知识点







正确答案
解析

设



考查方向
解题思路
根据三点共线定理,得到





易错点
三点共线定理的运用;根据

知识点
14.在平行四边形ABCD中,

正确答案
1
解析
设
如图
考查方向
解题思路
本题的解题思路
1)构造基底
2)使用三角形法则和平行四边形法则求出
3)根据数量积运算得出结果
易错点
本题易于错在数量积运算错误
知识点
10.对于两个平面向量



正确答案
解析
因为













考查方向
解题思路
.根据题中给出的运算公式分别带入选项逐个判断正误。
易错点
1.不会利用题中给出的新定义;2.对于新定义和我们学过的知识如何如何结合存在障碍。
知识点
15.在正方形





正确答案
[4,8-2
解析
设CN=x,CM=y,

因为

















考查方向
解题思路
画出正方形,设CN=x,CM=y,将

易错点
处理变量之间的整体关系及转化
知识点
已知向量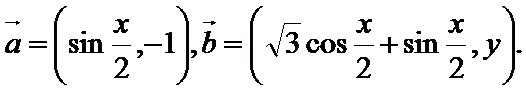
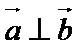
17.若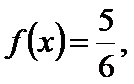
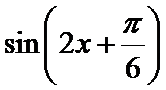
18.在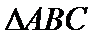
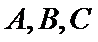
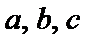
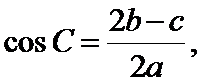
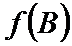
正确答案
解析
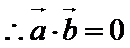
得
即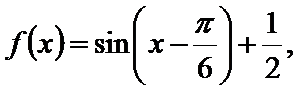
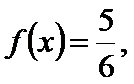
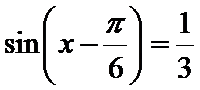
考查方向
解题思路
先通过向量垂直,得到三角关系,利用辅助角公式得到三角函数的解析式y=sin(x-
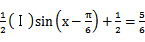
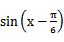

易错点
向量的坐标运算,三角函数的恒等变换
正确答案
(0,
解析
由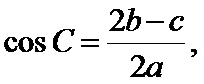
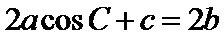
∴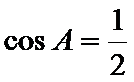

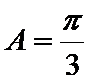
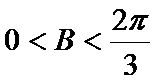
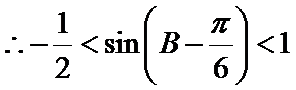
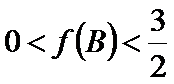
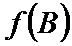
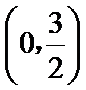
考查方向
解题思路
将边用正弦定理进行转化,得到cosA=


易错点
向量的坐标运算,三角函数的恒等变换
15.在正方形





正确答案
[4,8-2
解析
设CN=x,CM=y,

因为

















考查方向
解题思路
画出正方形,设CN=x,CM=y,将

易错点
处理变量之间的整体关系及转化
知识点
已知向量

17.若

18.在




正确答案
解析

得
即


考查方向
解题思路
先通过向量垂直,得到三角关系,利用辅助角公式得到三角函数的解析式y=sin(x-



易错点
向量的坐标运算,三角函数的恒等变换
正确答案
(0,
解析
由

∴







考查方向
解题思路
将边用正弦定理进行转化,得到cosA=


易错点
向量的坐标运算,三角函数的恒等变换
6.已知向量



正确答案
﹣3
解析
向量



可得
∴m﹣n=﹣3.
故答案为:﹣3
考查方向
解题思路
直接利用向量的坐标运算,求解即可.
易错点
本题考查向量的坐标运算,在线性计算过程易错.
知识点
扫码查看完整答案与解析