· 数列求和、数列的综合应用

· 其它方法求和

其它方法求和
共22题

· 数列求和、数列的综合应用

· 其它方法求和

其它方法求和
共22题

热门试卷

X 查看更多试卷

1

题型：简答题

|

简答题 · 12 分

17.已知是公差为3的等差数列，数列满足，.

（I）求的通项公式；

（II）求的前n项和.

正确答案

解：(1) ∵ anbn+1+bn+1=nbn ∴ n=1时 a1·b2+b2=b1

∴ a1· ∴ a1=2 由已知{an}乘以2为首项，公差3的等差数列

∴ an=a1+(n-1)·d=2+3(n-1) ∴ an=3n-1

(2)由①知代入

中∴ (3n-1)bn+1+bn+1=nbn

∴ (3n-1)bn+1+bn+1=nbn ∴ bn+1= (n∈n*)

∴ 设{bn}构成以1为首项，公比为的等比数列

∴ 设{bn}前n项和Sn，则Sn

知识点

等差数列的性质及应用等差数列的前n项和及其最值其它方法求和

1

题型：填空题

|

填空题 · 5 分

15．已知函数，记。设，若，则的最大值为。

正确答案

5

解析

解析已在路上飞奔，马上就到！

知识点

运用诱导公式化简求值其它方法求和数列与函数的综合数列与不等式的综合

1

题型：单选题

|

单选题 · 5 分

11．已知数列{an}的通项公式an =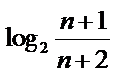(n∈N*)，设数列{an}的前n项和为Sn，则使Sn＜–5成立的自然数n （）

A有最大值63

B有最大值31

C有最小值63

D有最小值31

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

对数的运算性质其它方法求和数列与函数的综合

1

题型：简答题

|

简答题 · 18 分

已知递增的等差数列的首项，且、、成等比数列。

（1）求数列的通项公式；

（2）设数列对任意，都有成立，求的值。

（3）在数列中，，且满足，求下表中前行所有数的和.

……

…… ……

正确答案

（1）（2）（3）

解析

解析：（1）∵是递增的等差数列，设公差为 ……………………1分

、、成等比数列，∴ ……………………2分

由及得 ……………………………3分

∴ ……………………………4分

（2）∵，对都成立

当时，得 ……………………………5分

当时，由①，及②

①－②得，得 …………………7分

∴ …………………8分

∴ ……………10分

(3)∵ ∴

又∵ ∴ ………………………………13分

∵ ………………………………14分

∴第行各数之和

…………16分

∴表中前行所有数的和

知识点

其它方法求和等差数列与等比数列的综合

1

题型：简答题

|

简答题 · 16 分

若在数列中，，且对任意的，成等比数列，其公比为.

（1）若（），求.

（2）若对任意的，成等差数列，其公差为，设.

①求证：成等差数列；

②若，试求数列的前项和.

正确答案

见解析。

解析

（1），，是首项为1，公比为4的等比数列，

.

（2）①成等差数列，，又

，，则，得

，，即，

是公差为1的等差数列.

②，则由，解得或.

（ⅰ）当时，，，则，即，

得，所以，

则，

，则

（ⅱ）当时，，则，

即，得，

=

则，，从而.

综上所述，或。

知识点

等差数列的判断与证明其它方法求和等差数列与等比数列的综合

继续学习学习下一知识点

下一知识点 : 数列与函数的综合

百度题库 > 高考 > 文科数学 > 其它方法求和

扫码查看完整答案与解析