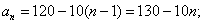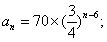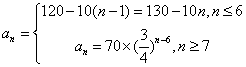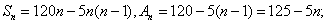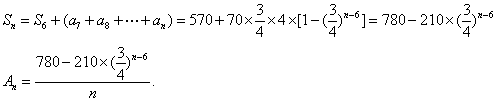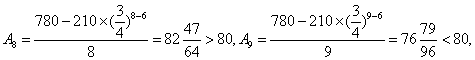- 数列与函数的综合
- 共58题
已知







(1)用


(2)求对所有


(3)当


正确答案
见解析
解析
(1)由已知得,交点A的坐标为
则抛物线在点A处的切线方程为:

(2)由(1)知f(n)=
即知,
特别地,当n=1时,得到a≥3
当a=3,n≥1时,
当n=0时,

所以满足条件的a的最小值为3.
(3)由(1)知f(k)=
下面证明:
首先证明0<x<1时,
设函数g(x)=6x(x2-x)+1,0<x<1, 则
当
故g(x)在区间(0,1)上的最小值
所以,当0<x<1时,g(x)>0,即得
由0<a<1知
知识点
已知函数

(1)求数列

(2)令

正确答案
见解析。
解析
(1)
当

(2)证明:由
又


知识点
某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少,从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%。
(1)求第n年初M的价值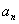
(2)设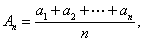
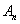
正确答案
见解析
解析
(1)当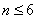
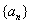
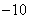
当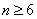
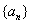
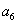
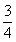
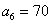
因此,第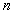
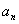
(2)设
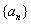
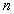
当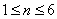
当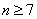
因为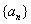
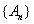
所以须在第9年初对M更新。
知识点
对于








(1)b2+b4+b6+b8=__;
(2)记cm为数列{bn}中第m个为0的项与第m+1个为0的项之间的项数,则cm的最大值是___.
正确答案
(1)3;(2)2.
解析
(1)观察知

一次类推





b2+b4+b6+b8=3;(2)由(1)知cm的最大值为2.
知识点
已知各项均不相同的等差数列


(1)求数列
(2)求数列
正确答案
(1)an=n+1(2)Tn=
解析
(1)设公差为d,由已知得
联立解得


故
(2)

知识点
扫码查看完整答案与解析