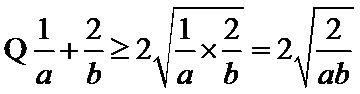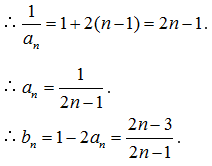- 基本不等式的实际应用
- 共15题
7.若实数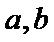
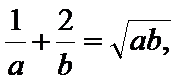
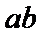
正确答案
解析
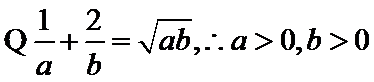

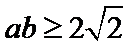
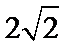
考查方向
解题思路
根据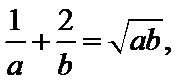
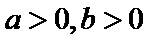
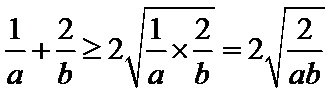
易错点
不会利用基本不等式得到
知识点
20.围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),
其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
正确答案
(Ⅰ)如图,设矩形的另一边长为a m,
则
由已知xa=360,得a=
(II)


即当x=24m时,修建围墙的总费用最小,最小总费用是10440元。
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知函数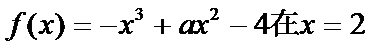

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知点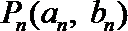


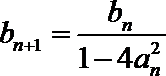

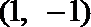
(1)求经过点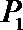

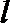
(2)已知点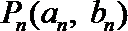





(3)在(2)的条件下,求对于所有


正确答案
(1)
(2)
(3)由(2)得
解析
解析已在路上飞奔,马上就到!
知识点
14.己知平行四边形的周长为6,则其对角线长的平方和的最小值是 .
正确答案
9
解析
试题分析:本题属于平面向量和基本不等式的问题,题目的难度较小。注意转化为平面向量求解。
考查方向
本题主要考查了平面向量和基本不等式的问题。
解题思路
本题考查平面向量,解题步骤如下:
设平行四边形的两邻边分别为向量a,b,夹角为θ。则对角线的平方和为
(a+b)2+(a-b)2=2a2+2b2≥(a+b)2=9。
易错点
本题必须注意转化为平面向量的问题求解,忽视则会出现错误。
知识点
扫码查看完整答案与解析