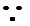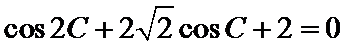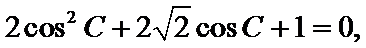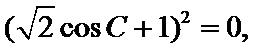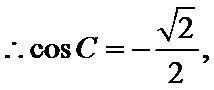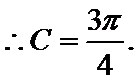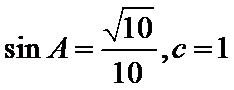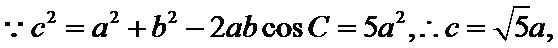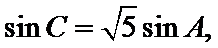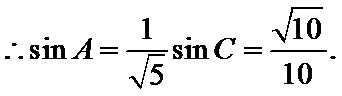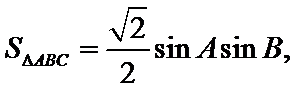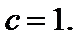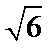- 正弦定理的应用
- 共30题
17.△ABC的内角A,B,C的对边分别别为a,b,c,已知
(I)求C;
(II)若

正确答案
解(Ⅰ)∵2cos C(acosB+bcosA)=C
∴2cos C(sinAcos B+sinBcosA)=sinC
∴2cosC sin(A+B)=sinC
∴2cosC sinC =sin C
∴
∴
∴
(Ⅱ) ∵△ABC面积为
∴
∴
∵a+b=5
∴a+b+c=5+
∴△ABC周长为5+
知识点
已知



17.若

18.若


正确答案
解析
试题分析:本题属于三角恒等变形和解三角形的基本问题,对

又


考查方向
解题思路
本题考查解三角形,解题步骤如下:对

易错点
对

正确答案

解析
试题分析:本题属于三角恒等变形和解三角形的基本问题,由方程思想求解出边长再算出面积;由17可知






考查方向
解题思路
本题考查解三角形,解题步骤如下:由方程思想求解出边长再算出面积。
易错点
根据条件合理选择定理来解三角形。
在




16.求
17.若


正确答案

解析
试题分析:本题属于向量的坐标运算、正余弦定理及三角形的面积公式的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:因为





考查方向
解题思路
利用向量

易错点
相关知识点不熟容易处错。
正确答案

解析
试题分析:本题属于向量的坐标运算、正余弦定理及三角形的面积公式的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
由余弦定理得,
化简得,




故

考查方向
解题思路
利用余弦定理求出a边,在利用面积公式即可求出

易错点
相关知识点不熟容易处错。
在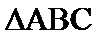
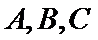
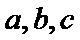
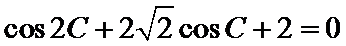
16.求角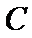
17.若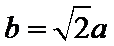
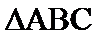

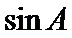

正确答案
(1) 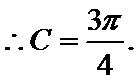
解析
(Ⅰ)
即
又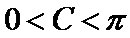
考查方向
解题思路
根据题中给出等式求出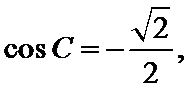
易错点
对于正弦定理的反复转化不明白。
正确答案
(2)
解析
(Ⅱ)
由正弦定理,得
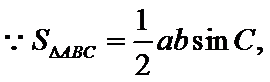
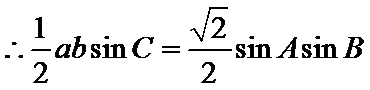
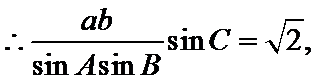
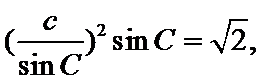
考查方向
解题思路
先根据余弦定理求出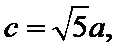
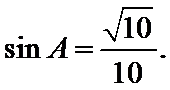
易错点
不知道该如何使用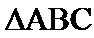
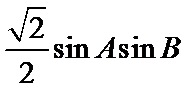
13.在
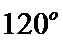
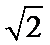
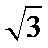
正确答案
解析
由正弦定理得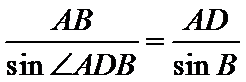
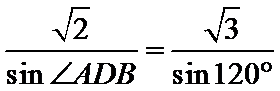
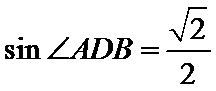

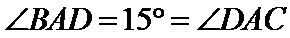
所以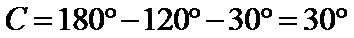
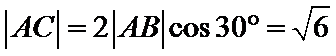
考查方向
解题思路
解三角形就是根据正弦定理和余弦定理得出方程进行的.当已知三角形边长的比时使用正弦定理可以转化为边的对角的正弦的比值,本例第一题就是在这种思想指导下求解的;当已知三角形三边之间的关系式,特别是边的二次关系式时要考虑根据余弦定理把边的关系转化为角的余弦关系式,再考虑问题的下一步解决方法.
易错点
边角关系的转化
知识点
扫码查看完整答案与解析