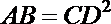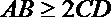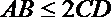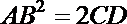- 正弦定理的应用
- 共30题
1
题型:简答题
|
19.在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域,点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船位于点A北偏东45º且与点A相距40




(1)求该船的行驶速度(单位:海里/小时)
(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
正弦定理的应用余弦定理的应用解三角形的实际应用
1
题型:
单选题
|
10.直角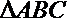
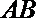
正确答案
B
解析
解析已在路上飞奔,马上就到!
知识点
正弦定理的应用
1
题型:简答题
|
已知函数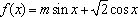
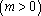
(1)求函数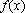
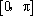
(2)已知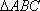
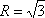
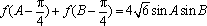
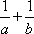
正确答案
(1)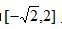
解析
(1)由题意,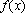
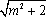
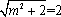
而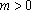
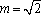
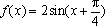
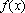
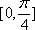
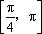
所以函数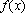
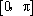
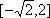
(2)化简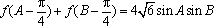
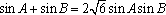
由正弦定理,得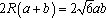
因为△ABC的外接圆半径为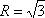
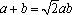
所以
知识点
正弦定理的应用
1
题型:简答题
|
设





(1)求实数

(2)
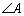







正确答案
见解析。
解析
(1)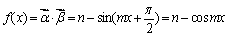
因为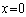
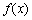
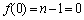
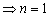
易知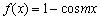

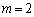

(2)由(Ⅰ)可知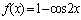
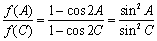
由正弦定理及余弦定理有: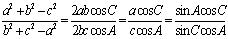
故
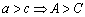
于是
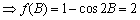
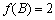
知识点
函数零点的判断和求解三角函数中的恒等变换应用正弦定理的应用三角函数的最值平面向量数量积的运算
1
题型:简答题
|
19. 在△ABC中,角A,B,C的对边分别为a,b,c,且满足(a-c) 
(1)求角B的大小;
(2)若|

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
三角函数的化简求值正弦定理的应用余弦定理的应用平面向量数量积的运算向量在几何中的应用
下一知识点 : 余弦定理
扫码查看完整答案与解析