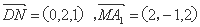异面直线及其所成的角
共54题

· 异面直线及其所成的角

异面直线及其所成的角
共54题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：单选题

单选题 · 5 分

（）·（4）=

正确答案

解析

知识点

异面直线及其所成的角

题型：简答题

简答题 · 12 分

底面边长为2的正三棱锥, 其表面展开图是三角形，如图.求△的各边长及此三棱锥的体积.

正确答案

解析

在△中，，所以是中位线，

故

同理，所以△是等边三角形，各边长均为4.

设Q是△ABC的中心，则PQ⊥平面ABC，

所以

从而，

知识点

异面直线及其所成的角

题型：填空题

填空题 · 4 分

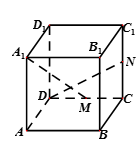
如图，在正方体中，、分别是、的中点，则异面直线与所成的角的大小是____________。

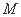
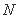
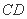
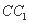
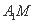
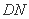
正确答案

90º

解析

方法一：连接D1M,易得DN⊥A1D1 ,DN⊥D1M,

所以，DN⊥平面A1MD1，

又A1M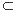平面A1MD1，所以，DN⊥A1D1，故夹角为90º

方法二：以D为原点，分别以DA, DC, DD1为x, y, z轴，建立空间直角坐标系D—xyz.设正方体边长为2，则D（0,0,0），N（0,2,1），M（0,1,0）A1（2,0,2）

故，

所以，cos<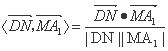 = 0,故DN⊥D1M，所以夹角为90º

知识点

异面直线及其所成的角

题型：简答题

简答题 · 12 分

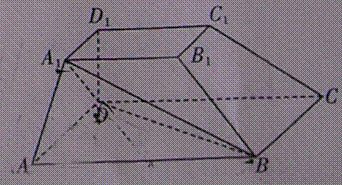
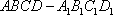
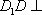
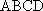
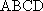
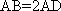
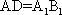
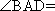
如图，在四棱台中，平面，底面是平行四边形，，，60°

（1）证明：；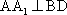

（2）证明：.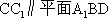

正确答案

见解析。

解析

（1）证明：因为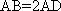，所以设

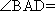
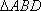
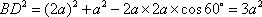
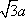
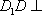
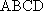
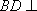
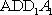
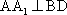
AD=a,则AB=2a,又因为60°,所以在中,由余弦定理得：,所以BD=,所以,故BD⊥AD,又因为

平面，所以BD,又因为, 所以平面,故.

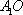
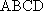
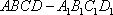
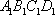
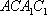
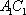
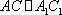
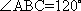
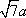
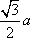
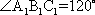
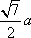
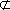
(2)连结AC,设ACBD=0, 连结,由底面是平行四边形得:O是AC的中点,由四棱台知:平面ABCD∥平面,因为这两个平面同时都和平面相交,交线分别为AC、，故，又因为AB=2a, BC=a, ，所以可由余弦定理计算得AC=，又因为A1B1=2a, B1C1=, ，所以可由余弦定理计算得A1C1=，所以A1C1∥OC且A1C1=OC，故四边形OCC1A1是平行四边形，所以CC1∥A1O，又CC1平面A1BD，A1O平面A1BD，所以.

知识点

异面直线及其所成的角空间中直线与直线之间的位置关系直线与平面平行的判定与性质直线与直线垂直的判定与性质

继续学习学习下一知识点

下一知识点 : 异面直线的判定

百度题库 > 高考 > 文科数学 > 异面直线及其所成的角

扫码查看完整答案与解析