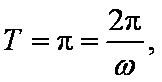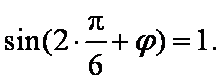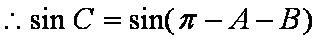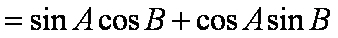- 二次函数与幂函数
- 共1316题
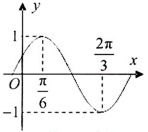
已知函数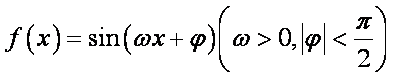
(1)求函数
(2)已知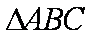

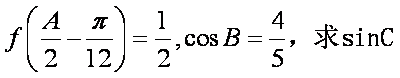
正确答案
见解析。
解析
(1)由周期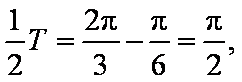
所以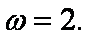
当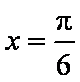
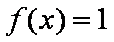
因为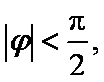
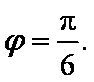
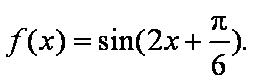
由图象可得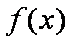
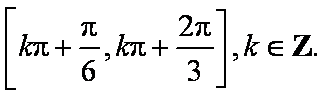
(2)由(1)可知,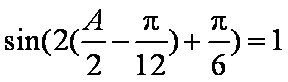
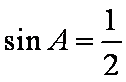
又角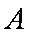
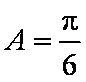
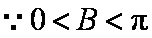
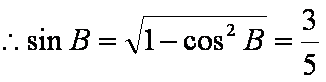
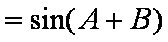
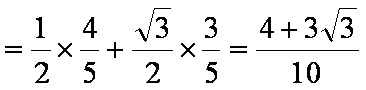
知识点
已知x=1是函数

(1)求m与n的关系式;
(2)求
正确答案
见解析
解析
解析(1)




(2)由(1)知,
当




故有上表知,当





当




故有上表知,当





知识点
已知椭圆



(1)求椭圆
(2)斜率为





正确答案
见解析。
解析
(1)设椭圆


由

∵ 椭圆经过点


∴ 椭圆的方程为
(2)设直线

由
令





知识点
已知函数



(1)求
(2)若
求证: 
正确答案
见解析
解析
(1)

当m<1时,



当
①当


②当


③当


综上

由题意得

(2),


由(1)知

知识点
如图所示,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F,FG切圆O于点G.
(1)求证:△DEF∽△EFA;
(2)如果FG=1,求EF的长。
正确答案
见解析
解析
(1)证明:


(2)
又因为FG为切线,则
所以,EF=FG=1.
知识点
已知函数
正确答案
解析
解析:令






将

由




故选:D
知识点
如图,某市准备在道路EF的一侧修建一条运动比赛道,赛道的前一部分为曲线段FBC,该曲线段是函数



(1)求

(2)若要在圆弧赛道所对应的扇形ODE区域内建一个“矩形草坪”,矩形的一边在道路OE上,一个顶点在半径OD上,另外一个顶点P在圆弧


正确答案
(1)
解析
(1)由条件,得

∵

∴ 曲线段FBC的解析式为
当x=0时,


(2)由(1),可知
又易知当“矩形草坪”的面积最大时,点P在弧DE上,故
设

=
∵

知识点
设函数
(1)若函数

①求实数a,b的值;
②求函数
(2)当b=0时,若不等式

正确答案
见解析
解析
(1)①




解得
②
当


令


(2)当b=0时,
若不等式

则

即

令






知识点
已知


正确答案
解析
解析:因为


函数


故选:A
知识点
如图,已知AB是⊙O的直径,AC是弦,AD⊥CE,垂足为D,AC平分∠BAD。
(1)求证:直线CE是⊙O的切线;
(2)求证:AC2=AB•AD。
正确答案
见解析
解析
证明:(1)连接OC,如下图所示:
因为OA=OC,
所以∠OCA=∠OAC,(2分)
又因为AD⊥CE,
所以∠ACD+∠CAD=90°,
又因为AC平分∠BAD,
所以∠OCA=∠CAD,(4分)
所以∠OCA+∠CAD=90°,
即OC⊥CE,
所以CE是⊙O的切线,(6分)
(2)连接BC,
因为AB是⊙O的直径,
所以∠BCA=∠ADC=90°,
因为CE是⊙O的切线,
所以∠B=∠ACD,(8分)
所以△ABC∽△ACD,
所以
即AC2=AB•AD,(10分)
知识点
扫码查看完整答案与解析