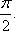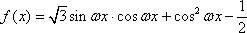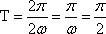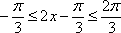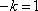- 二次函数与幂函数
- 共1316题
已知函数

(1)求常数
(2)在











正确答案
见解析。
解析
(1)
∵ 
∵ 函数


∴当



此时,
(2)∵
∴
∴ 

∵ 
∴ 
∵ 
∴
即
由①和②解得
∵
∴
知识点
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示。
(1)下表是年龄的频数分布表,求正整数
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率。
正确答案
见解析
解析
(1)由题设可知,

(2) 因为第1,2,3组共有50+50+200=300人,
利用分层抽样在300名学生中抽取
第1组的人数为
第2组的人数为
第3组的人数为
所以第1,2,3组分别抽取1人,1人,4人。………………6分
(2)设第1组的1位同学为





其中2人年龄都不在第3组的有:
所以至少有1人年龄在第3组的概率为
知识点
函数
正确答案
解析
略
知识点
已知函数






正确答案
解析
由
知识点
正确答案
解析
略
知识点
已知函数


(1)证明数列

(2)记

正确答案
见解析。
解析
(1)由已知得
∴数列
所以

(2) ∵

=
知识点
已知函数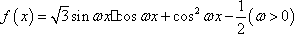
(1)求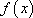
(2)将函数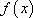
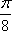
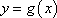

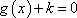
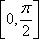
正确答案
见解析
解析
(1)
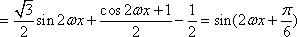
由题意知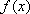
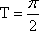
所以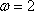
所以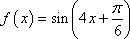
(2)将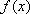
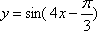
象所有点的横坐标伸长到原来的2倍,纵坐标不变,得到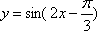
所以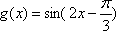
因为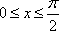
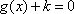
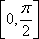
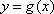
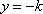
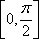
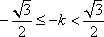
所以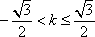
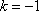
知识点
已知椭圆











(1)椭圆
(2)

正确答案
见解析
解析
(1)由题意可知





(2)设直线







即
∵

将①式代入②得:
当且仅当


知识点
给定下列四个命题:
①若一个平面内的两条直线与另外一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直。
其中,为真命题的是( )
正确答案
解析
①错, ②正确, ③错, ④正确.故选D
知识点
若对于定义在R上的函数f (x) ,其图象是连续不断的,且存在常数

f (x +






正确答案
①②
解析
略
知识点
扫码查看完整答案与解析