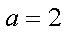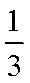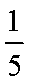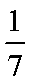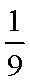- 二次函数与幂函数
- 共1316题
已知函数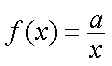
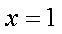
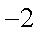
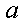
正确答案
2
解析
易得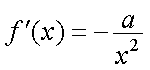
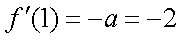
知识点
已知函数
(1)求
(2)求
(3)求

正确答案
见解析。
解析
(1)
所以最小正周期为
(2) 由 
整理,得

(3)当

故当x=0时,

知识点
某省高考数学阅卷点共有400名阅卷老师,为了高效地完成文、理科数学卷的阅卷任务,需将400名阅卷老师分成两组同时展开阅卷工作,一组完成269捆文科卷,另一组完成475捆理科卷,根据历年阅卷经验,文科每捆卷需要一位阅卷老师工作3天完成,理科每捆卷需要一位阅卷老师工作4天完成,(假定每位阅卷老师工作一天的阅卷量相同,每捆卷的份数也相同)
(1)如何安排文、理科阅卷老师的人数,使得全省数学阅卷时间最省?
(2)由于今年理科阅卷任务较重,理科实际每捆卷需要一位阅卷老师工作4.5天完成,在按(1)分配的人数阅卷4天后,阅卷领导小组决定从文科组抽调20名阅卷老师去阅理科卷,试问完成全省数学阅卷任务至少需要多少天?(天数精确到小数点后第3位)
(参考数据:



正确答案
见解析
解析
(1)设文科阅卷人数为

则阅卷时间为
而

答:当文、理科阅卷人数分别是119,281时,全省阅卷时间最省;
(2)文科阅卷时间为:
理科阅卷时间为:
答:全省阅卷时间最短为
知识点
已知函数
(1)求
(2)设



(3)设





正确答案
见解析。
解析
(1)

列表如下:
∵g(1) = 1,∴y =
(2)当


∵



设


∴

设


即
设

∴
∴
设


∴


∴

∴a≥3 


(3)由(1)知


∵

当


当



所以

此时


∴


由①②,得
∵

下证存在

取


设


∴


再证
∵

综上所述,

知识点
已知函数

正确答案
解析
验证可得
知识点
已知函数

(1)当


(2)当

(3)证明:对任意的

正确答案
见解析。
解析
(1)当


所以曲线


(2)


因为
(1)若

所以,


(2)若


所以,

………………………………………………………………………………………10分
(3)由(2)可知,当



以下分两种情况讨论:
(1)当


所以对任意
(2)当



若


若


所以,对任意
综上,对任意
知识点
已知椭圆



(1)求椭圆的方程;
(2)若





(3)在(2)的条件下,试问





正确答案
见解析
解析
(1)



(2)


直线


代入椭圆




(3)设存在



则由




知识点
已知
正确答案
(﹣1,2)
解析
∵
再根据f(x)在(0,+∞)上是增函数,f(0)=0,可得函数f(x)在R上是增函数。
令x2+x=12,求得x=3 或x=﹣4(舍去)。
∴由不等式f(x2﹣x+1)<12,可得 x2﹣x+1<3,即 (x+1)(x﹣2)<0,
解得﹣1<x<2,
知识点
在平面直角坐标系xoy中,已知曲线C1 
(1)将曲线C1上的所有点的横坐标,纵坐标分别伸长为原来的

(2)在曲线C2上求一点P,使点P到直线l的距离最大,并求出此最大值。
正确答案
见解析。
解析
(1)由题意知,直线l的直角坐标方程为:2x-y-6=0.
∵C2:(

(2)设P(
d=
∴当sin(60°-θ)=-1即点P(-


知识点
在游乐场,有一种游戏是向一个画满均匀方格的桌面上投硬币,若硬币恰落在任何一个方格内不与方格线重叠,即可获奖,已知硬币的直径为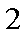
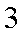
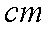
正确答案
解析
考查几何概型,游客获奖的概率为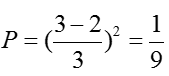
知识点
扫码查看完整答案与解析