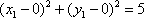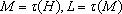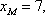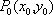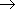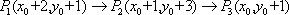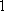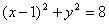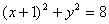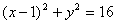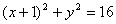- 圆的标准方程
- 共94题
已知圆C:

正确答案
解析
略
知识点
设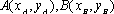
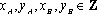
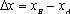
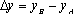
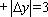
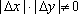
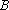
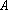
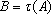
(1)请问:点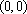
(2)已知点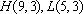
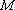
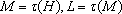
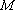
(3)已知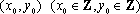
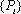
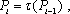
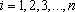
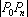
正确答案
见解析
解析
(1)因为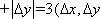
故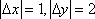
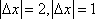
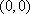

所以这些可能值对应的点在以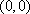

(2)设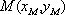
所以有
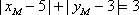
所以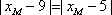
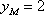
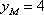
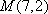
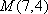
(3)当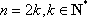
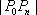
当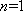
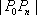

当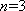

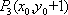
故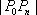
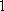
当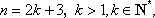

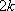
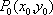
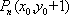
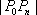
综上,当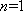
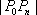
当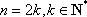
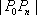
当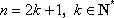
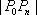
知识点
已知曲线





正确答案
解析
略
知识点
已知圆










(1)求直线
(2)求圆
正确答案
见解析。
解析
(1)(法一)∵点

∴直线


(法二)当直线

当直线




则圆心




∴直线

(2)设圆



∴圆

∵圆






整理得:


∵

∴圆

知识点
以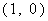
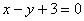
正确答案
解析
略
知识点
扫码查看完整答案与解析