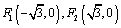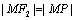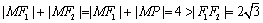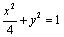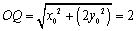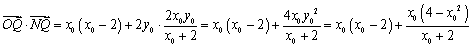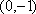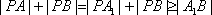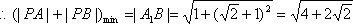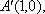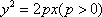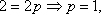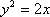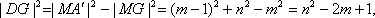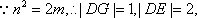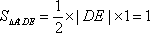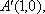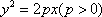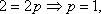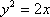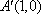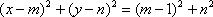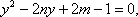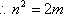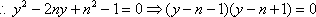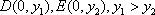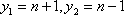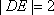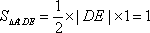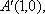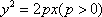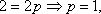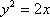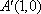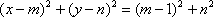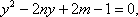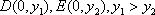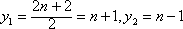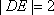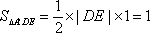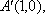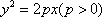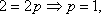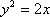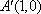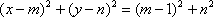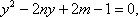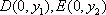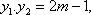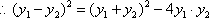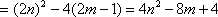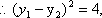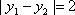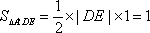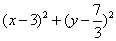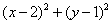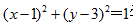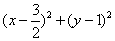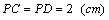- 圆的标准方程
- 共94题
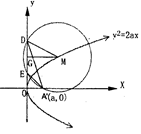
已知点P是圆F1: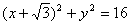
(1)求点M的轨迹C的方程;
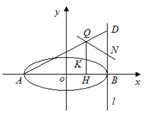
(2)设轨迹C与x轴的两个左右交点分别为A,B,点K是轨迹C上异于A,B的任意一点,KH⊥x轴,H为垂足,延长HK到点Q使得HK=KQ,连结AQ延长交过B且垂直于x轴的直线l于点D,N为DB的中点,试判断直线QN与以AB为直径的圆O的位置关系。
正确答案
见解析。
解析
(1)由题意得,
圆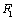
从而
∴ 点M的轨迹是以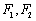
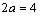
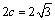
则短半轴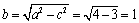
椭圆方程为:
(2)
设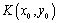
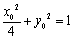
∵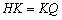
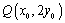
∴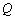
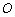
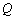
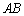
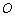
又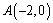
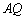
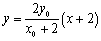
令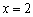
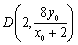
又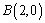
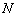
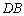
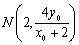
∴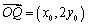
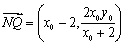
∴
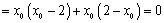
∴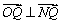
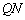
知识点
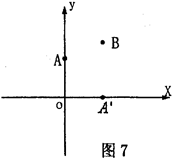
如图7,已知点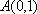
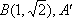
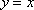

(1)求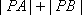
(2)已知抛物线C的顶点为原点O,焦点在
正确答案
见解析。
解析
(1)设点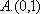
则A1的坐标为
于是
当且仅当A、P、B三点共线是取等号,
这时|PA|+|PB|取得最小值
(2)解法一:依题意知点
设抛物线C的方程为
由抛物线C过点B得
即抛物线C的方程为
过点M作y轴的垂线,垂足为G,则点G平分DE,
设圆心为M(m,n),
则
即当M运动时,弦DE的长不随圆心M的变化而变化,
又∵点A'到y轴的距离不变,∴三角形A'DE的面积不随圆心M的变化而变化,
解法二:依题意知点
设抛物线C的方程为
由抛物线C过点B得
即抛物线C的方程为
设圆的圆心为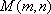
∴圆的方程为
令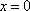
∵点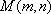
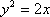
设
则
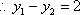
即当M运动时,弦DE的长不随圆心M的变化而变化,
又∵点A'到y轴的距离不变,∴三角形A'DE的面积不随圆心M的变化而变化;
解法三:依题意知点
设抛物线C的方程为
由抛物线C过点B得
即抛物线C的方程为
设圆的圆心为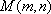
∴圆的方程为
令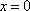
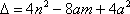
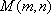
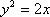
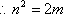
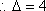
由求根公式得
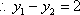
∴当M运动时,弦长|DE|为定值,
又∵点A'到y轴的距离不变,∴三角形A'DE的面积不随圆心M的变化而变化,
解法四:依题意知点
设抛物线C的方程为
由抛物线C过点B得
即抛物线C的方程为
设圆的圆心为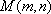
∴圆的方程为
令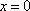
设
则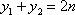
又∵点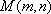
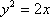
∴当M运动时,弦长|DE|为定值,又∵点A'到y轴的距离不变,
∴三角形A'DE的面积不随圆心M的变化而变化,
知识点
若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆的标准方程是
正确答案
解析
略
知识点
若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆的标准方程是
正确答案
解析
略
知识点
给定椭圆





(1)求椭圆C和其“准圆”的方程;
(2)过椭圆C的“准圆”与



(3)若点






正确答案
(1)
解析
(1)由题意知


故椭圆C的方程为


(2)由题意可得



则直线



由

所以直线



或直线



(3)由题意,可设

又A点坐标为

故

又

所以

知识点
如图,













正确答案
解析
略
知识点
若圆C的半径为1,圆心在第一象限,且与直线4x﹣3y=0和x轴相切,则该圆的标准方程是( )
正确答案
解析
设圆心为(a,1),由已知得

故选B
知识点
在极坐标系中,圆

正确答案
1
解析
略
知识点
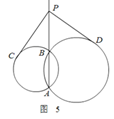
如图5,两圆相交于A、B两点,P为两圆公共弦AB上任一点,从P引两圆的切线PC、PD,若PC=2cm,则PD= ▲ cm.
正确答案
2
解析
:由切割线定理可得,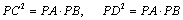
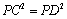
即
知识点
已知函数
(1)求曲线

(2)设函数

正确答案
见解析
解析
(1)当


所求切线方程为
(2)

根

当

在





当

在





知识点
扫码查看完整答案与解析