圆的一般方程
共16题

· 圆的一般方程

圆的一般方程
共16题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

已知椭圆的左右焦点分别为F1和F2，由4个点M（一a，b）、N（a，b）、F2和F1组成了一个高为，面积为3的等腰梯形．

（1）求椭圆的标准方程；

（2）过点F1的直线和椭圆交于两点A、B，求△F2AB面积的最大值。

正确答案

解析

知识点

圆的一般方程

题型：单选题

单选题 · 5 分

已知圆的方程为，则圆心坐标为

正确答案

解析

略

知识点

圆的一般方程

题型：单选题

单选题 · 5 分

设两圆、都和两坐标轴相切，且都过点，则两圆心的距离=

正确答案

解析

设，，则，，不妨设，则，，所以。

知识点

圆的一般方程

题型：填空题

填空题 · 5 分

一个几何体的三视图如图所示，则这个几何体的体积为__________.

正确答案

解析

略

知识点

圆的一般方程

题型：简答题

简答题 · 14 分

如图，椭圆的左顶点为，是椭圆上异于点的任意一点，点与点关于点对称。

（1）若点的坐标为，求的值；

（2）若椭圆上存在点，使得，求的取值范围。

正确答案

（1）

（2）

解析

（1）解：依题意，是线段的中点，

因为，，

所以点的坐标为。 ………………2分

由点在椭圆上，

所以， ………………4分

解得。 ………………6分

（2）解：设，则，且。 ① ………………7分

因为是线段的中点，

所以。 ………………8分

因为，

所以。 ② ………………9分

由 ①，② 消去，整理得。 ………………11分

所以， ………………13分

当且仅当时，上式等号成立。

所以的取值范围是。 ………………14分

知识点

圆的一般方程

题型：单选题

单选题 · 5 分

已知圆的方程为，设该圆过点的最长弦和最短弦分别为和，则四边形的面积为（）

正确答案

解析

略

知识点

圆的一般方程

题型：简答题

简答题 · 14 分

已知椭圆的右焦点为F，A为短轴的一个端点，且，的面积为1（其中为坐标原点）.

（1）求椭圆的方程；

（2）若C、D分别是椭圆长轴的左、右端点，动点M满足，连结CM，交椭圆于点，证明：为定值；

（3）在（2）的条件下，试问轴上是否存在异于点C的定点Q，使得以MP为直径的圆恒过直线DP、MQ的交点，若存在，求出点Q的坐标；若不存在，说明理由.

正确答案

见解析。

解析

(III)设.若以为直径的圆恒过的交点,

则.

由(2)可知:,

即恒成立,

∴存在，使得以为直径的圆恒过直线、的交点.……………14分

知识点

圆的一般方程

题型：简答题

简答题 · 14 分

已知函数。

（1）求曲线在点处的切线方程；

（2）若对于任意的，都有，求的取值范围。

正确答案

（1）

（2）

解析

（1） ------------------2分

， -----------------4分

∴曲线在处的切线方程为

，即， -----------------6分

（2）令得， -----------------2分

当变化时，和的变化情况如下表：

∴在上递减，在上递增 -----------------4分

∴在上的最小值是 -----------------6分

∴，即

∴的取值范围是， -----------------8分

知识点

圆的一般方程

题型：单选题

单选题 · 5 分

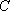
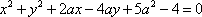
在平面直角坐标系内，若曲线：上所有的点均在第二象限内，则实数的取值范围为（）

正确答案

解析

略

知识点

圆的一般方程直线与圆的位置关系

题型：简答题

简答题 · 14 分

16.已知圆c以原点为圆心且经过点A（1，），直线l经过点和，

（1）求圆c的方程和直线l的一般方程；

（2）求与圆c相切且平行直线l的直线方程。

正确答案

略

解析

解析已在路上飞奔，马上就到！

知识点

直线的一般式方程圆的一般方程直线与圆的位置关系

继续学习学习下一知识点

下一知识点 : 轨迹方程的问题

百度题库 > 高考 > 文科数学 > 圆的一般方程

扫码查看完整答案与解析