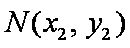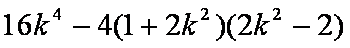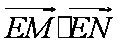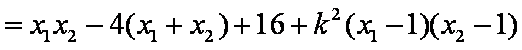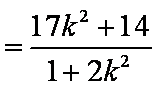圆的标准方程
共94题

· 圆的标准方程

圆的标准方程
共94题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 16 分

设动点到点和的距离分别为和，，若。

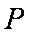
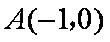
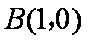
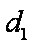
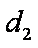
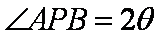
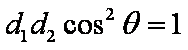
（1）求动点P的轨迹的方程；

（2）过点作直线交轨迹于两点，若，求的取值范围。

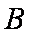
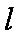
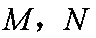
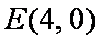
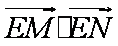
正确答案

见解析

解析

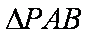
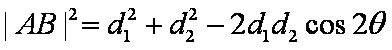
（1）在中由余弦定理得，

因为， ,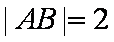

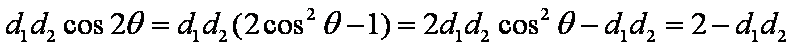
所以，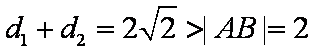

点P的轨迹C是以A、B为焦点的椭圆，其方程为.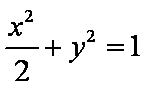

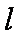
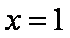
（2）(1)当直线的斜率不存在时，其方程为，

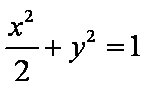
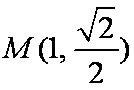
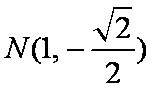
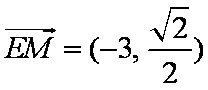
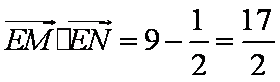
代入得，,

，，；

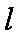
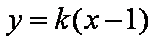
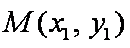
(2)当直线的斜率存在时，设其方程为，设，

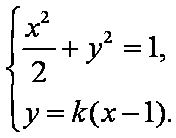
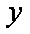
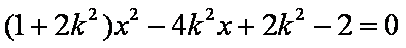
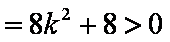
由消去得，

=

，

所以 ,

，,

，

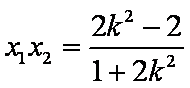
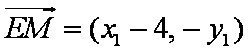
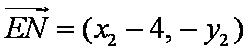
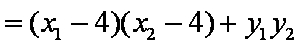
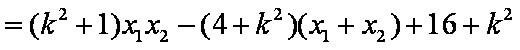
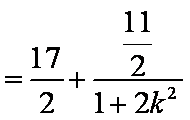
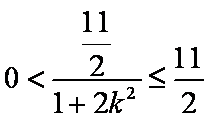
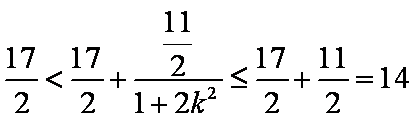
由于，所以，

当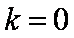时取等号,

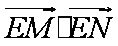
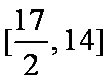
综上知的取值范围为.

知识点

圆的标准方程

题型：填空题

填空题 · 5 分

己知圆C的极坐标方程为则圆心C的一个极坐标为。

正确答案

解析

把极坐标方程为转化为直角坐标方程为：，所以圆心为，所以圆心C的一个极坐标为。

知识点

圆的标准方程

题型：简答题

简答题 · 13 分

已知圆C1的方程为，定直线l的方程为，动圆C与圆C1外切，且与直线l相切。

（1）求动圆圆心C的轨迹M的方程；

（2）斜率为k的直线l与轨迹M相切于第一象限的点P，过点P作直线l的垂线恰好经过点A（0，6），并交轨迹M于异于点P的点Q，记为POQ（O为坐标原点）的面积，求的值。

正确答案

见解析

解析

解（1）设动圆圆心C的坐标为，动圆半径为R，则

，且

可得。

由于圆C1在直线l的上方，所以动圆C的圆心C应该在直线l的上方，所以有，从而得，整理得，即为动圆圆心C的轨迹M的方程，

（2）如图示，设点P的坐标为，则切线的斜率为，可得直线PQ的斜率为，所以直线PQ的方程为，由于该直线经过点A（0,6），所以有，得，因为点P在第一象限，所以，点P坐标为（4,2），直线PQ的方程为

把直线PQ的方程与轨迹M的方程联立得，解得或4，可得点Q的坐标为，所以

知识点

圆的标准方程

题型：单选题

单选题 · 5 分

7.已知圆：+=1，圆与圆关于直线对称，则圆的方程为（）

A+=1

B+=1

C+=1

D+=1 [

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

圆的标准方程

题型：简答题

简答题 · 12 分

18．已知：以点为圆心的圆与轴交于点,与轴交于点，其中为原点。

（1）求证：的面积为定值；

（2）设直线与圆交于点，若，求圆的方程。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

圆的标准方程直线与圆的位置关系直线与圆相交的性质

继续学习学习下一知识点

下一知识点 : 圆的一般方程

百度题库 > 高考 > 文科数学 > 圆的标准方程

扫码查看完整答案与解析