- 棱柱的结构特征
- 共41题
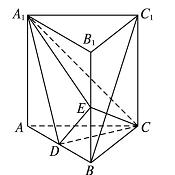
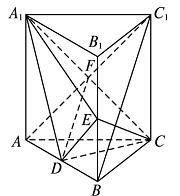
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点。
(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=2,AB=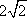
正确答案
见解析
解析
(1)连结AC1交A1C于点F,则F为AC1中点。
又D是AB中点,连结DF,则BC1∥DF.
因为DF⊂平面A1CD,BC1
所以BC1∥平面A1CD.
(2)
因为ABC-A1B1C1是直三棱柱,所以AA1⊥CD.
由已知AC=CB,D为AB的中点,所以CD⊥AB.
又AA1∩AB=A,于是CD⊥平面ABB1A1.
由AA1=AC=CB=2,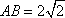
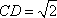
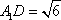
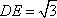
故A1D2+DE2=A1E2,即DE⊥A1D.
所以VC-A1DE=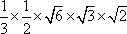
知识点
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB。
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD=
正确答案
略
解析
(1)证明:
因为

所以
因为
又
所以
(2)由(1)可知
在
又因为
所以四边形ABCE为矩形,
所以
又
所以
知识点
若曲线
正确答案
2
解析



知识点
椭圆C:


(1)求椭圆C的方程;
(2)如图,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意点,直线DP交x轴于点N直线AD交BP于点M,设BP的斜率为k,MN的斜率为m,证明2m-k为定值。
正确答案
见解析
解析



将①代入
又直线AD的方程为
①与②联立解得
由
所以MN的分斜率为m=

知识点
已知命题P: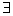
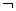
正确答案
解析
略
知识点
扫码查看完整答案与解析