- 棱柱的结构特征
- 共41题
已知曲线C的方程为:
(1)判断曲线C的形状;
(2)设曲线C分别与x轴、y轴交于点A、B(A、B不同于原点O),试判断△AOB的面积S是否为定值?并证明你的判断;
(3)设直线

正确答案
见解析。
解析
(1)将曲线C的方程化为
可知曲线C是以点

(2)△AOB的面积S为定值。
证明如下:
在曲线C的方程中令y=0得

在曲线C的方程中令x=0得

∴
(3)∵圆C过坐标原点,且
∴圆心


当


圆心到直线

直线
∴

知识点
如图,在直三棱柱



(1)求证:
(2)求三棱锥
正确答案
见解析。
解析
(1)由直三棱柱ABC-A1B1C1
得:
因为AC=AB ,所以A1B1= A1C1
在等腰
由面面垂直性质定理得:A1D⊥平面BB1C1C
又


(2)在
由直三棱柱AB

所以
由(1)知:点A1到面CB1D的距离为A1D =2
所以
综上:
知识点
如图,已知圆锥体






(1)求圆锥体的体积;
(2)异面直线

正确答案
见解析
解析
(1)由题意,

故
从而体积
(2)如图2,取


由





由


在


在



则



知识点
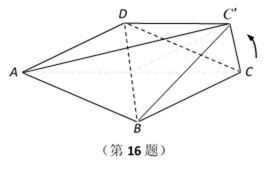
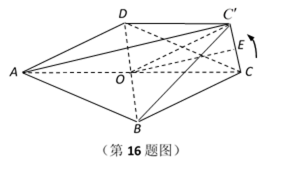
如图,在边长为1的菱形ABCD中,将正三角形BCD沿BD向上折起,
折起后的点C记为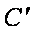
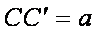
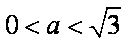
(1)若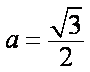
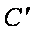
(2)当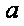
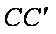
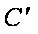
正确答案
见解析
解析
(1)
连结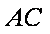
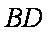
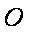
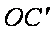
菱形ABCD中,
因三角形BCD沿BD折起,所以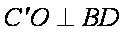
故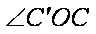
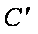
易得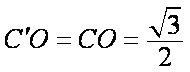
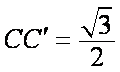
所以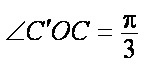
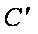
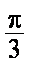
(2)当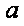
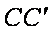
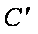
因为E,O分别为线段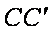
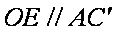
又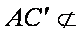
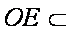
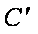
知识点
如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有( )。
正确答案
解析
设正方体的棱长为a.建立空间直角坐标系,如图所示。
则D(0,0,0),D1(0,0,a),C1(0,a,a),C(0,a,0),B(a,a,0),B1(a,a,a),A(a,0,0),A1(a,0,a),P
则|

|

|

|


|


|

故共有4个不同取值,故选B.
知识点
扫码查看完整答案与解析