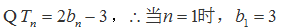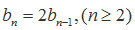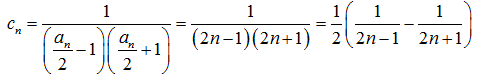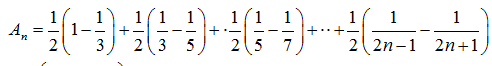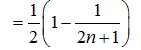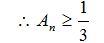- 数列求和、数列的综合应用
- 共397题
17.在数列

(1)求数列
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知等比数列






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.等差数列


(1)求

(2)若数列


正确答案
(1)
(2)


解析
解析已在路上飞奔,马上就到!
知识点
15.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列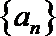
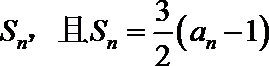
(I)求数列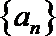
(II)设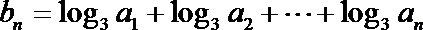
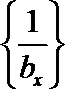
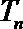
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列


(1)求证数列

(2)求数列





正确答案
(1)∵
∴ 

∴ 数列
∴ 
(2)∵ 
∴
∵
又
∴ 

∴ 当

要使得

结合(1)的结果,只需
∴ 正整数
解析
解析已在路上飞奔,马上就到!
知识点
19.对于数列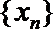
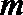
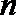
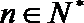
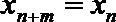
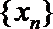
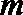
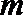
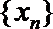
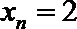
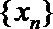
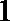
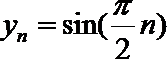
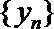
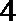
(Ⅰ)设数列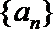
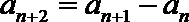
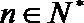
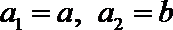
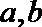
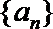
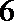
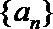
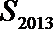
(Ⅱ)设数列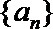
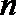
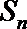
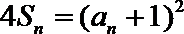
①若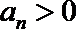
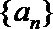
②若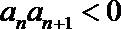
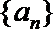
(Ⅲ)设数列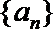
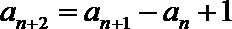
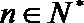
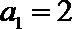
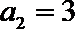
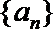
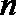
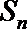
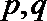
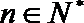
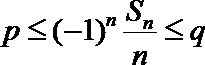
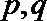
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知数列




正确答案
解析








考查方向
解题思路
详见解析
易错点
不能够想到

知识点
18. 已知数列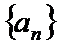
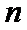
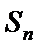
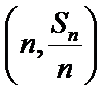
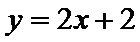
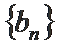
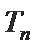
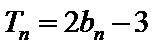
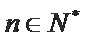
(Ⅰ)求数列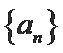
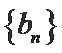
(Ⅱ)设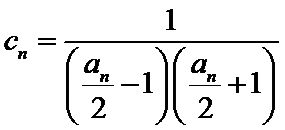
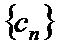
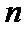
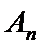
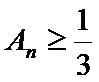
正确答案
(1)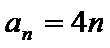
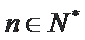
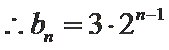
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
解:(Ⅰ)由题意,得 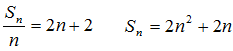
当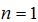
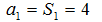
当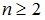
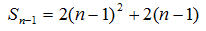
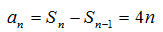
综上,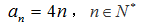
又
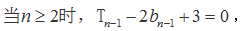
数列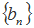
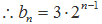
(Ⅱ)
考查方向
解题思路
本题考查数列问题,解题步骤如下:
1、利用an与Sn的关系求解。
2、利用等比数列的求和公式求解。
易错点
等比数列分项时项数易错。
知识点
18.已知函数

(1)求数列
(2)


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析