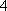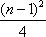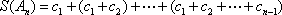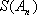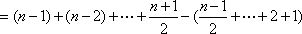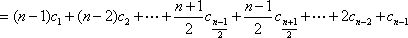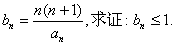- 数列求和、数列的综合应用
- 共397题
已知数列{an}的前n项和
正确答案
解析
已知数列{an}的前n项和
∴an=Sn﹣Sn﹣1=n2﹣3n﹣[(n﹣1)2﹣3(n﹣1)]=2n﹣4,
n=1满足an,
∴an=2n﹣4,
∵它的第k项满足2<ak<5,即2<2k﹣4<5,解得3<k<4.5,因为n∈N,
∴k=4,
故选C;
知识点
已知函数



(1)求数列{

(2)






(3)令
正确答案
见解析。
解析
知识点
已知数列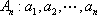
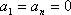
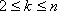
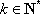
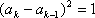
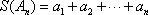
(1)写出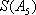
(2)求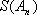
正确答案
(1)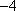
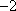

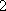
(2)
解析
(1)由题设,满足条件的数列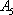
1)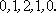
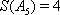
2)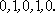
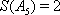
3)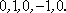
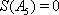
4)
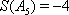
5)
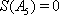
6)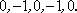
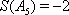
所以,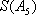
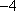
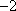

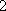
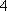
(2)由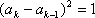
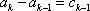
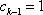
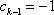
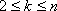
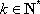
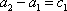

…
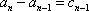
所以
因为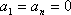



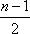
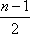
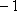
所以

则当
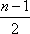
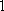
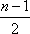
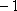
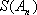
此时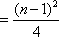
证明如下:
假设
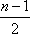

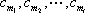
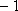



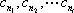
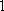

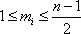
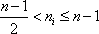
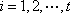
所以
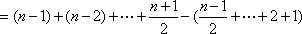
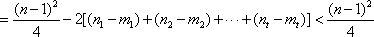
所以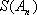
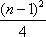
知识点
在等比数列



(1)求数列
(2)若






正确答案
见解析。
解析
因为数列

所以

故
而
所以
整理得
所以
所以
(2) 数列

所以
故
因为
所以
所以当

求
令
此时二次函数

故当



知识点
已知各项均不相等的等差数列


(1)求数列
(2)设





正确答案
见解析。
解析
(1)设数列


又
解得:
所以
(2)
所以
故存在常数
知识点
已知函数



(1)求数列{

(2)






(3)令
正确答案
见解析。
解析
知识点
已知等比数列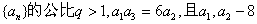
(1)求数列{an}的通项公式;
(2)设
正确答案
见解析。
解析
知识点
已知数列


(1)求数列
(2)设



正确答案
见解析。
解析
知识点
已知点(1,2)是函数


(1)求数列
(2)将数列

正确答案
见解析。
解析
(1)把点(1,2)代入函数


当

当

经验证可知

(2)由(1)知数列


∴此数列的和为
又数列

∴所求剩余项的和为
知识点
对于每一个正整数





正确答案
-2
解析
知识点
扫码查看完整答案与解析