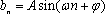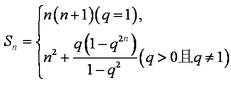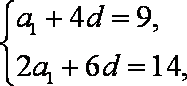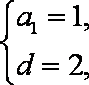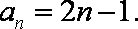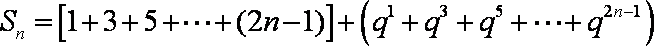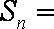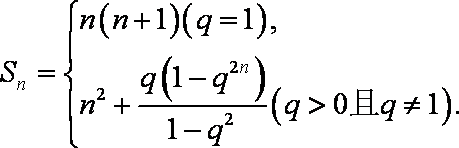- 数列求和、数列的综合应用
- 共397题
已知数列




正确答案
解析
略
知识点
已知数列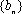
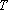
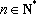
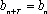
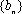
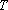
数列



数列
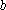

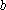
数列
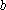


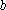

(1)对于数列②,它的一个通项公式可以是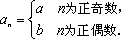
(2)求数列③的前
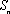
(3)在数列③中,若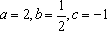
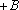
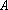
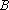

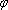
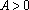
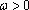
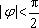
正确答案
见解析
解析
(1)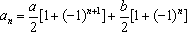
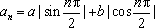
(2)当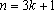
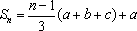
当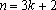
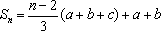
当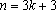
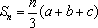
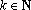
(3)由题意,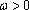
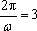
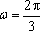
于是
把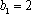
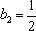
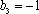
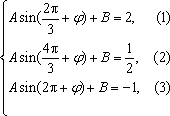
由(1)(2)可得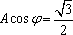
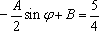
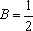
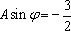
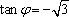
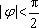
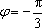
于是可求得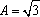
故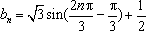
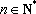
或写成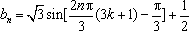
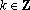
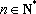
知识点
设数列
(1)求数列
(2)设



正确答案
(1)
(2)
解析
(1)设等比数列







(2) 


知识点
已知数列{an}的相邻两项an,an+1是关于x的方程x2﹣2nx+bn=0(n∈N*)的两实根,且a1=1。
(1)求证:数列
(2)设Sn是数列{an}的前n项和,求Sn;
(3)问是否存在常数λ,使得bn>λSn对∀n∈N*都成立,若存在,求出λ的取值范围,若不存在,请说明理由。
正确答案
见解析。
解析
(1)证明:∵an,an+1是关于x的方程x2﹣2n•x+bn=0(n∈N*)的两实根,
∴
∵
故数列

(2)由(1)得
即


(3)由(2)得
要使bn>λSn,对∀n∈N*都成立,
即
①当n为正奇数时,由(*)式得:
即
∵2n+1﹣1>0,∴
故
∴λ<1。
②当n为正偶数时,由(*)式得:
∵2n﹣1>0,∴
故

∴
知识点
数列


(1)求数列
(2)若数列




正确答案
见解析
解析
解析:(1)当

当


(2)当
当

则
知识点
已知等差数列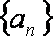

(1)求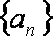
(2)若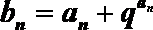
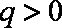
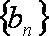
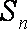
正确答案
(1)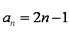
解析
解析:(1)设
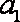
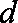
由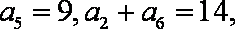
解得
所以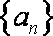
(2)由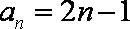
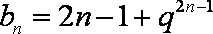
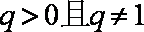
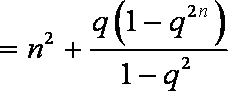
② 当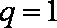
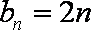
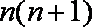
所以数列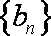
知识点
12.已知数列






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.对于三次函数f(x)=ax3+bx2+cx+d(a≠0),定义:设f″(x)是函数y=f(x)的导数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点为函数y=f(x)的“拐点”。有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,求:
(1)函数f(x)=x3-3x2+3x对称中心为___________;
(2)若函数

正确答案
(1,1) ; 2010
解析
解析已在路上飞奔,马上就到!
知识点
12.已知

正确答案
2008
解析
解析已在路上飞奔,马上就到!
知识点
20.数列{an}中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*)。
(1)求数列{an}的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn。
正确答案
解:(1)由an+2=2an+1-an
d=
(2)由an=10-2n≥0可得n≤5,当n≤5时,Sn=-n2+9n,当n>5时,Sn=n2-9n+40,故Sn=
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析