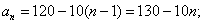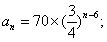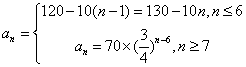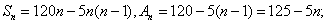- 数列求和、数列的综合应用
- 共397题
17.已知数列



(1)求

(2)记数列


正确答案
(1)


解析
试题分析:(1)利用等比数列的通项公式求出


(2)利用错位相减法求和即可。
(1) 由


∵


当n≥2时,

即

(2)由(1)可得
∴

∴
考查方向
解题思路
(1)直接由








(2)求出


易错点
错位相减法求和时的计算,分类讨论的思想的应用.
知识点
设数列{an}(n=1,2,3…)的前n项和Sn满足Sn=2an-a3,且a1,a2+1,a3成等差数列.
16.求数列的通项公式;
17.设数列
正确答案
an=2n;
解析
由已知Sn=2an-a1,有
an=Sn-Sn-1=2an-2an-1(n≥2)
即an=2an-1(n≥2)
从而a2=2a1,a3=2a2=4a1,
又因为a1,a2+1,a3成等差数列
即a1+a3=2(a2+1)
所以a1+4a1=2(2a1+1),解得a1=2
所以,数列{an}是首项为2,公比为2的等比数列
故an=2n.
考查方向
解题思路
1.第(1)问先根据题中给出的条件得到an=2an-1(n≥2),然后再求出a1=2,即可求出an=2n.
易错点
1.不会根据Sn=2an-a3求出an=2an-1(n≥2);
正确答案
Tn=
解析
由上题得
所以Tn=
考查方向
解题思路
第(2)问根据第(1)问的结论直接求解即可。
易错点
.求前n项和时对于项数出错。
18. 已知数列


(Ⅰ)求

(Ⅱ)设



正确答案
(1)


解析
试题分析:本题属于等差数列及数列的求和,
(1)直接利用公式来解答;
(2)先利用裂项相消法求出
(Ⅰ)设数列


由

所以

(Ⅱ)可得

由于

即

考查方向
解题思路
本题考查等差数列及数列的求和,解题步骤如下:(1)直接利用公式来解答;(2)先利用裂项相消法求出
易错点
第二问求和不晓得使用裂项相消法去做。
知识点
16.设



正确答案
解析
∵
∴当


当


∴
故答案为
考查方向
解题思路
由





易错点
要分清n是奇数和偶数.
知识点
《消防法》规定,生产易燃易爆危险物品的单位,对产品应当( )。
A.附有燃点数据的说明书
B.附有闪点数据的说明
C.附有爆炸极限数据的说明书
D.附有安全标志的说明书
E.注明防火防爆注意事项
正确答案
A,B,C,E
解析
暂无解析
已知







(1)用


(2)求对所有


(3)当


正确答案
见解析
解析
(1)由已知得,交点A的坐标为
则抛物线在点A处的切线方程为:

(2)由(1)知f(n)=
即知,
特别地,当n=1时,得到a≥3
当a=3,n≥1时,
当n=0时,

所以满足条件的a的最小值为3.
(3)由(1)知f(k)=
下面证明:
首先证明0<x<1时,
设函数g(x)=6x(x2-x)+1,0<x<1, 则
当
故g(x)在区间(0,1)上的最小值
所以,当0<x<1时,g(x)>0,即得
由0<a<1知
知识点
已知函数

(1)求数列

(2)令

正确答案
见解析。
解析
(1)
当

(2)证明:由
又


知识点
某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少,从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%。
(1)求第n年初M的价值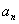
(2)设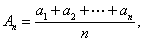
正确答案
见解析
解析
(1)当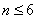
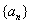
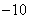
当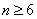
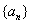
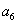
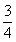
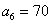
因此,第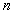
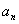
(2)设
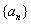
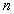
当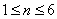
当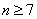
因为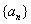
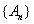
所以须在第9年初对M更新。
知识点
对于








(1)b2+b4+b6+b8=__;
(2)记cm为数列{bn}中第m个为0的项与第m+1个为0的项之间的项数,则cm的最大值是___.
正确答案
(1)3;(2)2.
解析
(1)观察知

一次类推





b2+b4+b6+b8=3;(2)由(1)知cm的最大值为2.
知识点
已知各项均不相同的等差数列


(1)求数列
(2)求数列
正确答案
(1)an=n+1(2)Tn=
解析
(1)设公差为d,由已知得
联立解得


故
(2)

知识点
扫码查看完整答案与解析