- 数列求和、数列的综合应用
- 共397题
已知数列






正确答案

解析
略
知识点
数列




正确答案
解析
略
知识点
给定有限单调递增数列









(1)判断数列




(2)若数列

①数列


②若



正确答案
见解析
解析
(1)数列



对于数列














(2)①取







②由①知,数列





假设


此时取








当


知识点
设等差数列{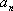
(1)求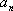
(2)设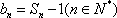
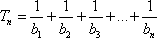
正确答案
见解析。
解析
知识点
数列{an}的前n项和为Sn,若a1=1,an+1=3Sn(n≥1),则a6=( )
正确答案
解析
由an+1=3Sn⇒Sn+1-Sn=3Sn⇒Sn+1=4Sn,所以数列{Sn}是首项为1,公比为4的等比数列,所以Sn=4n-1,所以a6=S6-S5=45-44=3×44,所以选择A.
知识点
正项等比数列{an}的前n项和为Sn,a4 =16,且a2,a3的等差中项为S2。
(1)求数列{an}的通项公式;
(2)设
正确答案
见解析。
解析
知识点
数列{an}的首项为3,{bn}为等差数列且bn=an+1-an(n∈N*),若b3=-2,b10=12,则a8=( )
正确答案
解析
由数列{bn}为等差数列,且b3=-2,b10=12可知数列公差d=2,所以通项bn=-2+(n-3)×2=2n-8=an+1-an,所以a8-a1=2×(1+2+3+…+7)-8×7=0,所以a8=a1=3.
知识点
已知等比数列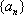
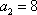
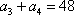
(1)求数列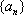
(2)设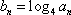
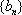
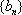

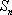
正确答案
见解析
解析
(1)解:设等比数列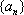
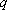
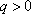
因为 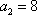
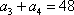
两式相除得 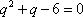
解得 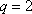
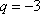
所以 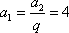
所以数列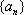
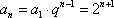
(2)解:由(1)得 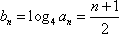
因为 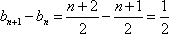
所以数列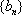
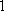
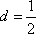
所以 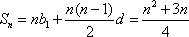
知识点
已知



(1)求数列{an}和数列{bn}的通项公式;
(2)将数列{bn}中的第a1项,第a2项,第a3项,……,第an项,……删去后剩余的项按从小到大的顺序排成新数列(cn},求数列{cn}的前2013项的和。
正确答案
见解析。
解析
知识点
已知








(1)求数列

(2)将数列







正确答案
见解析。
解析
(1)

因为

所以

解得:


(2)由题知将数列





知识点
扫码查看完整答案与解析











