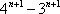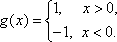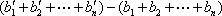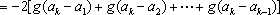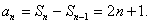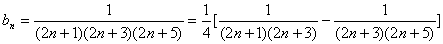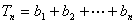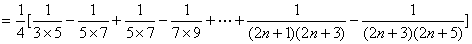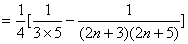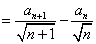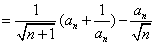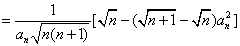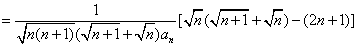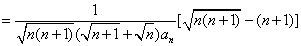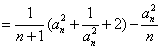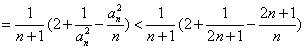- 数列求和、数列的综合应用
- 共397题
正确答案
解析
略
知识点
已知集合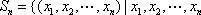

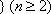
对于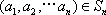

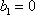
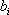
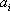
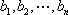
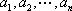
(1)当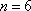
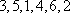
(2)证明:若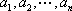
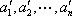
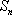
(3)对于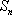
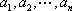
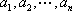
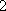
正确答案
见解析
解析
(1)解:当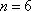

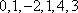
(2)证明:设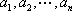
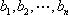
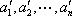
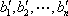
从右往左数,设排列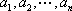
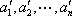
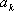
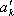
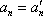
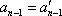

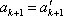
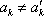
显然 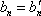
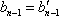

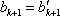
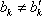
由满意指数的定义知,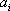
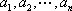
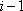
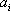
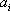
由于排列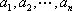
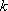
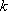
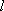
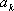
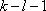
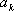
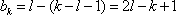
同理,设排列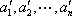
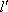
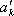
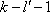
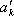
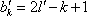
因为 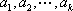
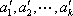
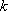
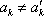
所以 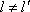
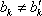
所以排列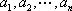
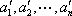
(3)证明:设排列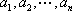
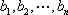
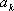
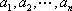
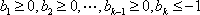
依题意进行操作,排列
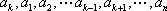
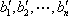
所以
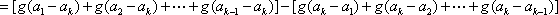
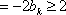
所以,新排列的各项满意指数之和比原排列的各项满意指数之和至少增加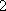
知识点
已知数列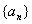
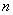
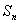
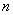
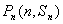
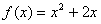
(1)求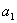
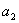
(2)求数列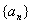
(3)若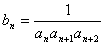
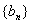
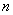
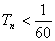
正确答案
见解析。
解析
(1)∵点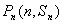
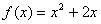
∴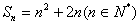
∴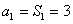
又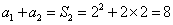
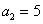
(2)由(1)知,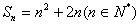
当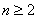
由(1)知,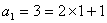
所以数列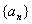
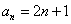
(3)由(2)得
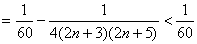
知识点
正确答案
见解析。
解析
知识点
设数列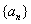
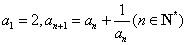
(1)证明: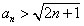
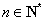
(2)令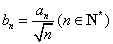
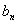
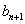
正确答案
见解析。
解析
(1)证法一:当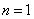
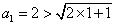
假设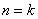
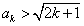
当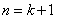
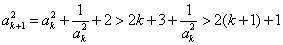
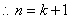
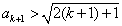
综上由数学归纳法可知, 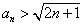
证法二:当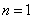
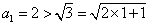
假设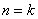
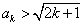
当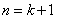
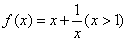
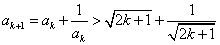
因此只需证: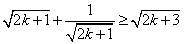
而这等价于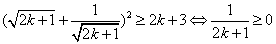
显然成立,所以当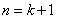
综上由数学归纳法可知,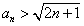
(2)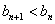
证法一: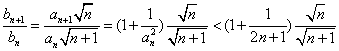
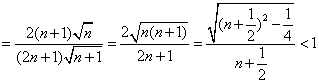
又显然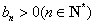
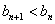
证法二: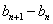
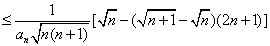
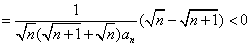
所以
证法三: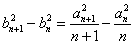

故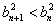
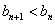
知识点
已知在等比数列
(1)若数列


(2)求数列

正确答案
见解析。
解析
知识点
已知





正确答案
解析
略
知识点
已知数列





正确答案
解析
略
知识点
设等比数列{

(1)求数列{
(2)在

(I)在数列{

(II)求证:
正确答案
见解析。
解析
(1)由
可得:
两式相减:
又
因为数列


所以
(2)由(1)可知
因为:

(Ⅰ)假设在数列


则:


因为

(*)可以化简为

所以在数列


(Ⅱ)令

两式相减:

知识点
各项均为正数的等比数列{an}中,已知a1=2,a5= 512,Tn是数列{log2an}的前n项和。
(1)求数列{an}的通项公式;
(2)求Tn;
(3)求满足
正确答案
见解析。
解析
知识点
扫码查看完整答案与解析