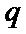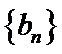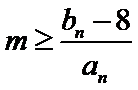- 数列求和、数列的综合应用
- 共397题
18.
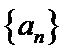
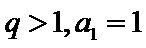
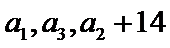
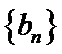
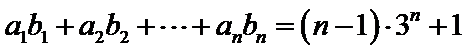
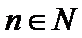
(I)求数列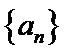
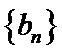
(II)若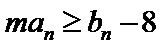
正确答案
见解析
解析
考查方向
解题思路
1)借助等差数列性质求出
2)利用由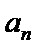
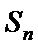
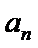
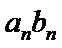
3)对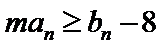
4)讨论新数列单调性,并求出最值
易错点
本题第一问忽略验证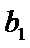
知识点
16.已知数列{an}满足a1


正确答案
解析
易知=+1,∴+1=2(+1).
又a1=1,∴+1=(+1)

当

∴bn+1-bn=(n-λ)2n-(n-1-λ)

又n∈N*,∴λ<2.
考查方向
解题思路
1)由

2)由数列单调性的定义求
易错点
本题易根据函数的单调性判断数列的单调性,忽略数列自变量的特殊性;
知识点
已知等比数列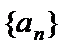
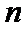
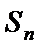
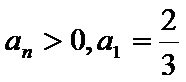
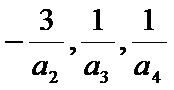
22.求数列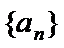
23.设数列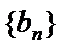
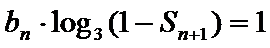
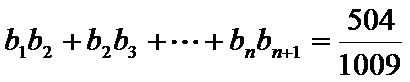
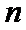
正确答案
(Ⅰ)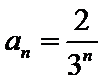
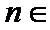

解析
(Ⅰ)设等比数列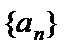
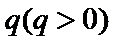
∵ 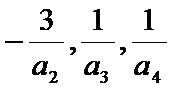
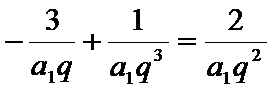
∴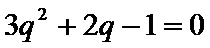
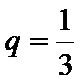
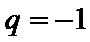
∴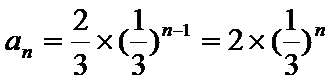
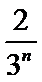
∴数列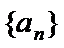
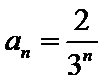
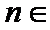

考查方向
解题思路
先根据题中给出的条件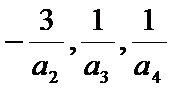
易错点
对于题中给出的条件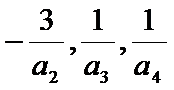
正确答案
(Ⅱ)
解析
(Ⅱ)由(Ⅰ)知,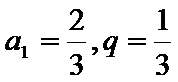
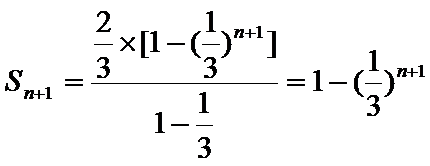
∵数列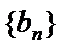
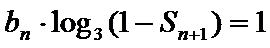
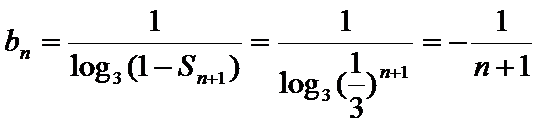
∴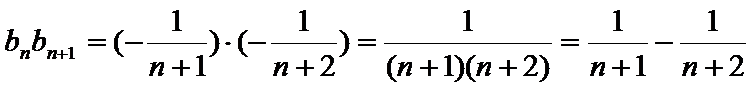
∴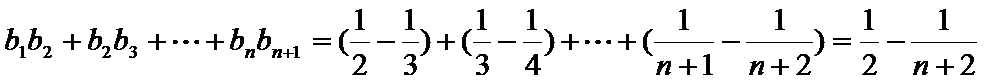
由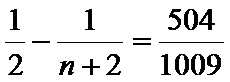
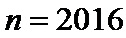
∴满足方程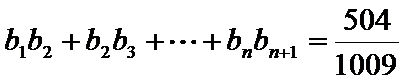
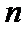
考查方向
解题思路
1.先根据题中给出的条件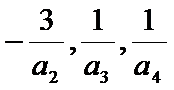
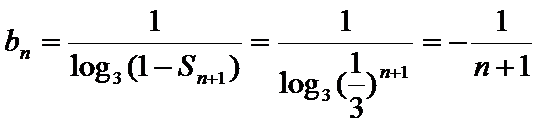
易错点
1.对于题中给出的条件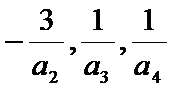
16. 设








正确答案
解析
f(
























考查方向
解题思路
可利用倒序相加求
易错点
求

知识点
23.一青蛙从点





(1)若点




(2)若点




(3)若点





正确答案
(1)设
所以

(2)依题意,
随着

横向路程之和无限接近
所以 
(注:只要能说明横纵坐标的变化趋势,用文字表达也行)
(3)设点


其中

∴


∴
即当


又
∴当

∴

解析
解析已在路上飞奔,马上就到!
知识点
21.设数列






(Ⅰ) 求数列
(Ⅱ)是否存在实数


正确答案
(Ⅰ)由题意可得:



①─②得



(Ⅱ)解法一:
若
则
得
又


故存在实数

解法二:
欲使


故存在实数

解析
解析已在路上飞奔,马上就到!
知识点
已知数列{an}的前n项和为Sn,且满足:a1=a(a≠0),an+1=rSn(n∈N*,r∈R,r≠-1),
(1)求数列{an}的通项公式;
(2)若存在k∈N*,使得Sk+1,Sk,Sk+2成等差数列,试判断:对于任意的m∈N*,且m≥2,am+1,am,am+2是否成等差数列,并证明你的结论。
正确答案
见解析。
解析
(1)由已知an+1=rSn,可得an+2=rSn+1,两式相减可得
an+2-an+1=r(Sn+1-Sn)=ran+1,即an+2=(r+1)an+1,
又a2=ra1=ra,所以
当r=0时,数列{an}为:a,0,…,0,…;
当r≠0,r≠-1时,由已知a≠0,所以an≠0(n∈N*),
于是由an+2=(r+1)an+1,可得
∴a2,a3,…,an,…成等比数列,
∴当n≥2时,an=r(r+1)n-2a.
综上,数列{an}的通项公式为
(2)对于任意的m∈N*,且m≥2,am+1,am,am+2成等差数列,证明如下:
当r=0时,由(1)知,
∴对于任意的m∈N*,且m≥2,am+1,am,am+2成等差数列;
当r≠0,r≠-1时,∵Sk+2=Sk+ak+1+ak+2,Sk+1=Sk+ak+1,
若存在k∈N*,使得Sk+1,Sk,Sk+2成等差数列,则Sk+1+Sk+2=2Sk,
∴2Sk+2ak+1+ak+2=2Sk,即ak+2=-2ak+1,
由(1)知,a2,a3,…,an,…的公比r+1=-2,于是对于任意的m∈N*,
且m≥2,am+1=-2am,从而am+2=4am,
∴am+1+am+2=2am,即am+1,am,am+2成等差数列。
综上,对于任意的m∈N*,且m≥2,am+1,am,am+2成等差数列。
知识点
已知曲线











(1)求

(2)判断
(3)求证:
正确答案
见解析。
解析
(1)由已知过


直线交曲线C于另一点
所以
即

所以
(2)解:当

因为
注意到


由于

当

当
(3)由于

所以

所以
所以


所以
知识点
19.已知数列{










(Ⅰ)求数列{



(Ⅱ)设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
已知等差数列









23.求数列

24.记

正确答案
解析
(1)由





从而

在已知
当





考查方向
解题思路
先解一元二次方程可得


易错点
熟悉已知递推关系求数列通项公式的方法
正确答案


考查方向
解题思路
求出数列
易错点
熟悉求差比较法
扫码查看完整答案与解析