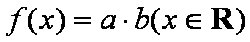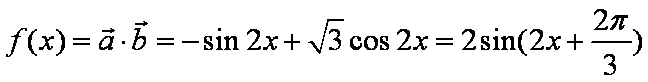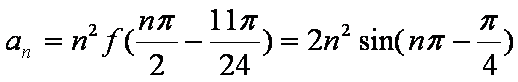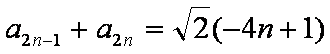- 数列求和、数列的综合应用
- 共397题
12.观察下列等式:




……
照此规律,
正确答案
知识点
16.数列




正确答案
15
解析


考查方向
解题思路
先化简数列
易错点
不知道数列
知识点
在FIDIC合同条件中,可索赔工期和费用,但不可以索赔利润的索赔事件包括( )。
A.业主延误移交施工现场
B.业主提前占用工程
C.工程师延误发放图纸时间
D.不可预见的外界条件
E.施工中遇到文物
正确答案
D,E
解析
暂无解析
23.一青蛙从点





(1)若点




(2)若点




(3)若点





正确答案
(1)设
所以

(2)依题意,
随着

横向路程之和无限接近
所以 
(注:只要能说明横纵坐标的变化趋势,用文字表达也行)
(3)设点


其中

∴


∴
即当


又
∴当

∴

解析
解析已在路上飞奔,马上就到!
知识点
7 .已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知数列

正确答案
解析
根据题意可知,
考查方向
三角函数,数列求和
解题思路
先表示出数列的前几项,然后找到规律求解数列的和
易错点
相关公式掌握混淆
知识点
已知数列{an}的前n项和为Sn,且满足:a1=a(a≠0),an+1=rSn(n∈N*,r∈R,r≠-1),
(1)求数列{an}的通项公式;
(2)若存在k∈N*,使得Sk+1,Sk,Sk+2成等差数列,试判断:对于任意的m∈N*,且m≥2,am+1,am,am+2是否成等差数列,并证明你的结论。
正确答案
见解析。
解析
(1)由已知an+1=rSn,可得an+2=rSn+1,两式相减可得
an+2-an+1=r(Sn+1-Sn)=ran+1,即an+2=(r+1)an+1,
又a2=ra1=ra,所以
当r=0时,数列{an}为:a,0,…,0,…;
当r≠0,r≠-1时,由已知a≠0,所以an≠0(n∈N*),
于是由an+2=(r+1)an+1,可得
∴a2,a3,…,an,…成等比数列,
∴当n≥2时,an=r(r+1)n-2a.
综上,数列{an}的通项公式为
(2)对于任意的m∈N*,且m≥2,am+1,am,am+2成等差数列,证明如下:
当r=0时,由(1)知,
∴对于任意的m∈N*,且m≥2,am+1,am,am+2成等差数列;
当r≠0,r≠-1时,∵Sk+2=Sk+ak+1+ak+2,Sk+1=Sk+ak+1,
若存在k∈N*,使得Sk+1,Sk,Sk+2成等差数列,则Sk+1+Sk+2=2Sk,
∴2Sk+2ak+1+ak+2=2Sk,即ak+2=-2ak+1,
由(1)知,a2,a3,…,an,…的公比r+1=-2,于是对于任意的m∈N*,
且m≥2,am+1=-2am,从而am+2=4am,
∴am+1+am+2=2am,即am+1,am,am+2成等差数列。
综上,对于任意的m∈N*,且m≥2,am+1,am,am+2成等差数列。
知识点
已知曲线











(1)求

(2)判断
(3)求证:
正确答案
见解析。
解析
(1)由已知过


直线交曲线C于另一点
所以
即

所以
(2)解:当

因为
注意到


由于

当

当
(3)由于

所以

所以
所以


所以
知识点
已知向量a,b满足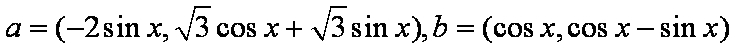
(1)将
(2)已知数列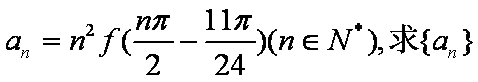
正确答案
见解析。
解析
(1)
(2)
则
所以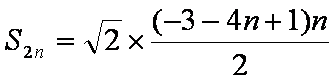
知识点
19.已知数列{










(Ⅰ)求数列{



(Ⅱ)设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析