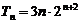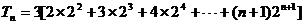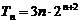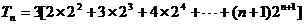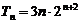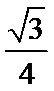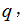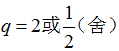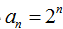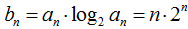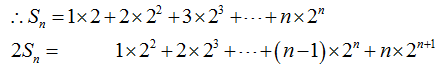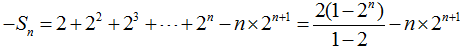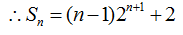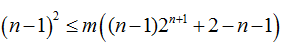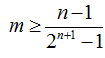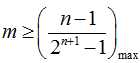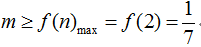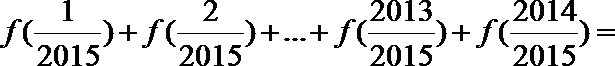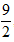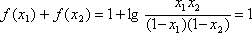- 数列求和、数列的综合应用
- 共397题
19. 已知数列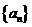
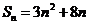
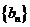
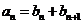
(I)求数列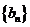
(II)令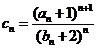
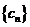
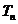
正确答案
(Ⅰ)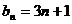
解析
试题分析:(Ⅰ)由题意得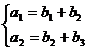
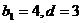
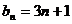
(Ⅱ)由(Ⅰ)知
利用“错位相减法”即得
试题解析:(Ⅰ)由题意当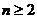
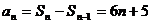
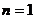
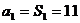
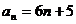
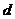
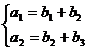
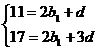

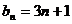
(Ⅱ)由(Ⅰ)知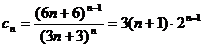
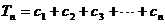
,所以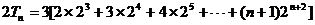
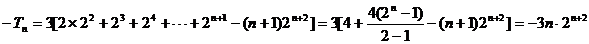
所以
考查方向
知识点
19. 已知单调递增的等比数列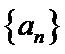
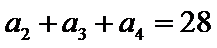
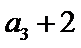
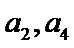
(I)求数列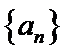
(II)设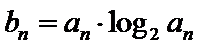
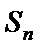
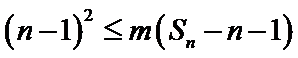
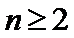
正确答案
(1)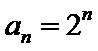
(2)
解析
试题分析:本题属于数列应用中的基本问题,题目的难度是逐渐由易到难,直接按照步骤来求
(Ⅰ)设等比数列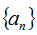
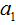
由题意可知: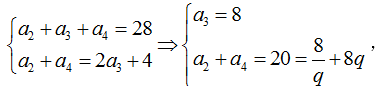
∴
所以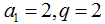
(Ⅱ)令
相减得
若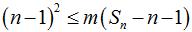
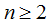
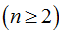
令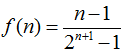
考查方向
解题思路
本题考查数列的性质,解题步骤如下:
1、利用基本量法求出通项;
2、利用错位相减法求和,恒成立问题转为最值问题
易错点
第一问中的辅助角容易计算错误
知识点
17.已知函数

(1)求
(2)求
(3)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数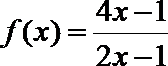

正确答案
4028
解析
解析已在路上飞奔,马上就到!
知识点
已知函数
正确答案
解析
略
知识点
设函数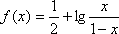
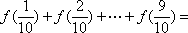
正确答案
解析
若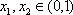
故
知识点
函数
正确答案
解析
略
知识点
设函数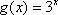
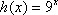
(1)解方程:
(2)令
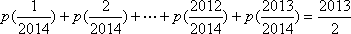
(3)若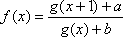
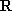
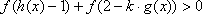


正确答案
见解析
解析
(1)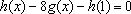
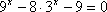
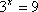
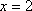
(2)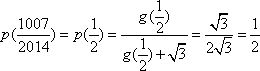
因为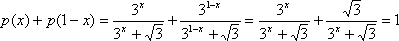
所以,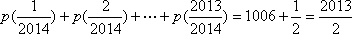
(3)因为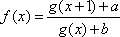
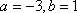
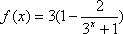
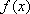
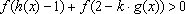
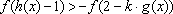


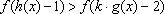
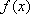
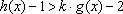
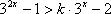
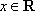
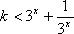
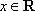
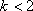
知识点
5.已知

正确答案
2046
解析
解析已在路上飞奔,马上就到!
知识点
13. 对于三次函数







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析