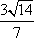- 进行简单的合情推理
- 共19题
设















正确答案
解析
略
知识点
已知集合







(1)当




(2)(ⅰ)证明:若



(ⅱ)设



说明理由;
(3)记




正确答案
见解析
解析
(1)解:当

得 

由 


(2)(ⅰ)证明:设


因为 

所以 

即 


所以 

所以

(ⅱ)解:设



反例如下:取


则 



因为

所以不存在

(3)解法一:因为 
设






所以
因为 
所以 

所以 
因为

又 
所以

即 
对于 





综上,

解法二:首先证明如下引理:设

证明:因为 

所以 
即 
所以

上式等号成立的条件为


对于 





综上,

知识点
设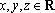
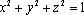


正确答案
解析
略
知识点
若存在正实数




① 



其中“在
正确答案
②③
解析
略
知识点
在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”,类似的,我们在平面向量集





①若
②若
③若

④对于任意向量
其中真命题的序号为
正确答案
解析
略
知识点
已知

整数,且



正确答案
41
解析
略
知识点
对于两个图形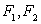
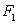
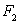
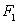
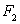
①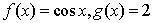
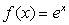
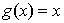
③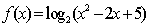
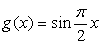
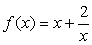
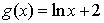
⑤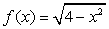
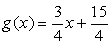
正确答案
②④
解析
略
知识点
某珠宝店丢了一件珍贵珠宝,以下四人中只有一人说真话,只有一人偷了珠宝. 甲:我没有偷;乙:丙是小偷;丙:丁是小偷;丁:我没有偷. 根据以上条件,可以判断偷珠宝的人是( )
正确答案
解析
略
知识点
对于集合


正确答案
解析
略
知识点
15. 数学与文学之间存在着许多奇妙的联系. 诗中有回文诗,如:“云边月影沙边雁,水外天光山外树”,倒过来读,便是“树外山光天外水,雁边沙影月边云”,其意境和韵味读来真是一种享受!数学中也有回文数,如:88,454,7337,43534等都是回文数,无论从左往右读,还是从右往左读,都是同一个数,称这样的数为“回文数”,读起来还真有趣!
二位的回文数有11,22,33,44,55,66,77,88,99,共9个;
三位的回文数有101,111,121,131,…,969,979,989,999,共90个;
四位的回文数有1001,1111,1221,…,9669,9779,9889,9999,共90个;
由此推测:10位的回文数总共有________个.
正确答案
90000
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析