- 抛物线焦点弦的性质
- 共78题
20.在直角坐标系

(I)求
(II)除H以外,直线MH与C是否有其它公共点?说明理由.
正确答案
解:将直线l与抛物线联立
(1) ∵ M关于P的对称点为N ∴ 

∴ ON直线斜率
则H点坐标

∴
(2)由①知
与抛物线联立

即y2-4ty=4t2 

∴ 直线MH与曲线C除点H外没有其它公共点
知识点
5. 设F为抛物线C:y2=4x的焦点,曲线y=
正确答案
知识点
20.
已知抛物线C:y2=2x的焦点为F,平行于x轴的两条直线l1,l2分别交C于A,B两点,交C的准线于P,Q两点.
(Ⅰ)若F在线段AB上,R是PQ的中点,证明AR∥FQ;
(Ⅱ)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程.
正确答案
(Ⅰ)由题设



记过



(Ⅰ)由于


记




所以
(Ⅱ)设


则
由题设可得


设满足条件的

当



而

当




知识点
如图,在平面直角坐标系


34.若直线


35.已知抛物线



①求证:线段

②求
正确答案

解析



即抛物线的焦点为

考查方向
解题思路
易错点
抛物线方程的形式,设而不求的思想。直线与抛物线的位置关系的运算程序。
正确答案
① 设点
则:

又

即
又




解析
① 设点
则:

又

即
又




② 






考查方向
解题思路
易错点
抛物线方程的形式,设而不求的思想。直线与抛物线的位置关系的运算程序。
7.已知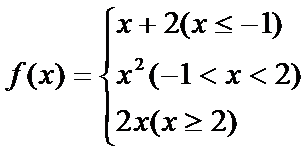
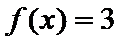
正确答案
解析
若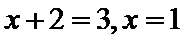
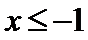
若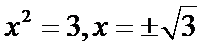
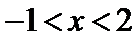
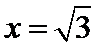
若

综上可知,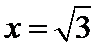
知识点
14.过抛物线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知符号函数sgn(x)= 
正确答案
解析
当x>1时,ln x>0,sgn(ln x)=1;
当x=1时,ln x=0,sgn(ln x)=0;
当0<x<1,ln x<0,sgn(ln x)=-1,
∴f(x)=sgn(ln x)-ln x=
知识点
10.设抛物线





正确答案
解析
设准线为









(1)当点P在第一象限时,






(2)当点P在第四象限时,






考查方向
解题思路
1.对P点进行分类;
2.对每一类情况,由抛物线的定义加以解决,应选C。
易错点
1.不能正确利用抛物线的定义,作出解答;
2.想不到对P点要分类讨论。
知识点
扫码查看完整答案与解析