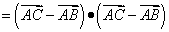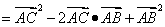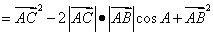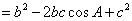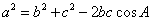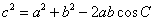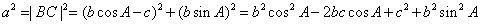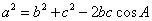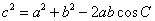抛物线的有关应用
共18题

· 抛物线的有关应用

抛物线的有关应用
共18题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

16．有限集合中元素的个数记作．已知，，，，且，．若集合满足，则集合的个数是；若集合满足，且，，则集合的个数是．（用数字作答）

正确答案

256； 672

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的有关应用

题型：填空题

填空题 · 4 分

14．已知函数（为常数）．若在区间上是增函数，则的取值范围是_________ 。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的有关应用

题型：单选题

单选题 · 5 分

8．正方体中，点是底面正方形内的一个动点，若直线，所成的角等于，则以下说法正确的是（）

A点的轨迹是圆的一部分

B点的轨迹是椭圆的一部分

C点的轨迹是双曲线的一部分

D点的轨迹是抛物线的一部分

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的有关应用

题型：简答题

简答题 · 12 分

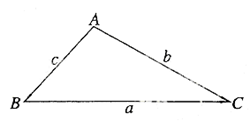
叙述并证明余弦定理。

正确答案

见解析。

解析

叙述：

余弦定理：三角形任何一边的平方等于其他两遍平方的和减去这两边与它们夹角的余弦之积的两倍。或：在△ABC中，a，b，c为A，B，C的对边，有

，

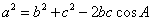
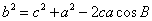
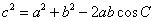
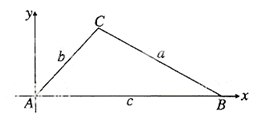
证明：（证法一）

如图，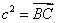

即

同理可证，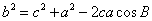

（证法二）

已知中，所对边分别为，以为原点，所在直线为轴建立直角坐标系，则，

∴

，

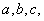
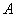
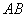
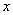
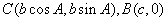
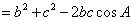
即

同理可证，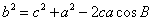

知识点

抛物线的有关应用

题型：简答题

简答题 · 18 分

（1）设椭圆：与双曲线：有相同的焦点，是椭圆与双曲线的公共点，且的周长为，求椭圆的方程；

我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.

（2）如图，已知“盾圆”的方程为.设“盾圆”上的任意一点到的距离为，到直线的距离为，求证：为定值；

（3）由抛物线弧：（）与第（1）小题椭圆弧：（）所合成的封闭曲线为“盾圆”.设“盾圆”上的两点关于轴对称，为坐标原点，试求面积的最大值.

正确答案

见解析

解析

（1）由的周长为得，

椭圆与双曲线：有相同的焦点，所以，

即，，椭圆的方程；…………………4分

（2）证明：设“盾圆”上的任意一点的坐标为，.………5分

当时，，，

即；…………………………7分

当时，，，

即；…………………………9分

所以为定值；

（3）因为“盾圆”关于轴对称，设于是，

所以面积，………………………………………………………11分

按点位置分2种情况：

①当在抛物线弧（）上时，

设所在的直线方程（），

联立，得，同理，

面积，所以；………………14分

②当在椭圆弧上时， [来源:学_科_网]

于是联立，得；

即，由，

当且仅当等号成立，所以，…………………………………17分

综上等腰面积的最大值为.

知识点

抛物线的有关应用

题型：简答题

简答题 · 12 分

已知函数。

（1）求的值；

（2）若，求。

正确答案

（1）1

（2）

解析

（1）

（2），，

。

知识点

抛物线的有关应用

题型：单选题

单选题 · 5 分

已知向量共线，那么的值为（）.

正确答案

解析

，其与共线，则，解得，

则.

知识点

抛物线的有关应用

题型：填空题

填空题 · 4 分

11．若不等式对于任意正整数恒成立，则实数的取值范围是（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的有关应用

题型：填空题

填空题 · 5 分

选做题（14、15题，只能从中选做一题）

14. （坐标系与参数方程选做题）

曲线极坐标方程为，以极点为原点，极轴为轴正半轴建立直角坐标系，直线参数方程为（为参数），则曲线上的点到直线距离最小值为__________.

15.（几何证明选讲选做题）

如图，是半径为的⊙的直径，是弦，，的延长线交于点，，则__________.

正确答案

14.

15.

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的有关应用

题型：单选题

单选题 · 5 分

8．数列的向若按如下规律排列：

若存在正整数k，使=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的有关应用

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 文科数学 > 抛物线的有关应用

扫码查看完整答案与解析