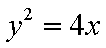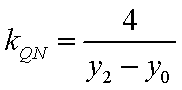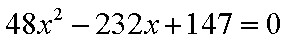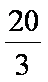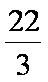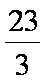- 空间几何体的三视图、表面积和体积
- 共1381题
已知定点A(1,0), B为x轴负半轴上的动点,以AB为边作菱形ABCD,使其两对 角线的交点恰好落在y轴上。
(1)求动点D的轨迹五的方程。
(2)若四边形MPNQ的四个顶点都在曲线E上,M,N关于x轴对称,曲线E在M点处的切线为l,且PQ//l
①证明直线PN与QN的斜率之和为定值;
②当M的横坐标为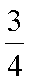
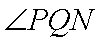
正确答案
见解析。
解析
(1) 设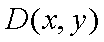
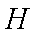
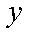
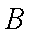
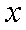
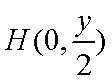
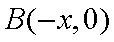
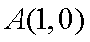
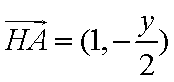
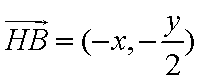
又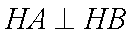
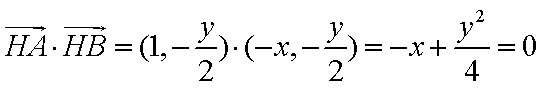
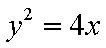
而
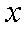
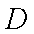
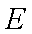
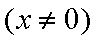
(2) ①设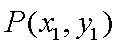
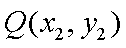
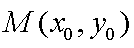
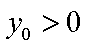
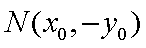
则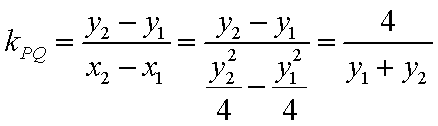
同理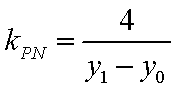
而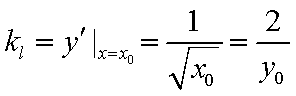
因为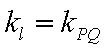
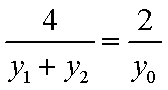
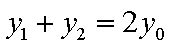
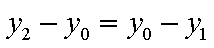
所以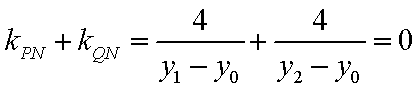
(8分)
② 因为
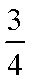
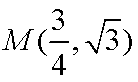
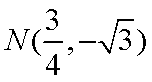
由于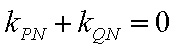
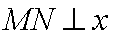
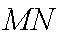
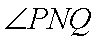
而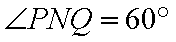
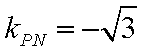
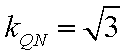
从而直线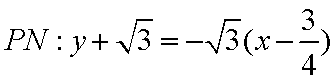
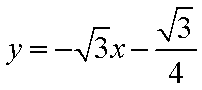
直线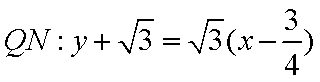
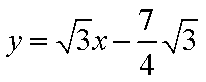
由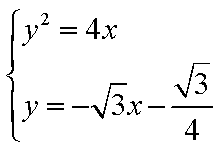
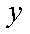
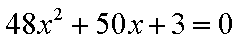
所以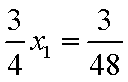
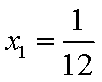
同理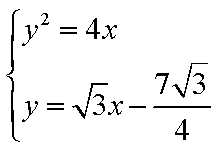
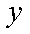
所以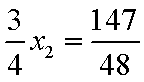
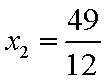
因此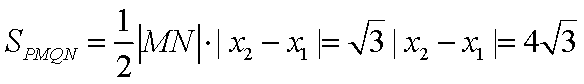
知识点
已知i为虚数单位,复数

正确答案
解析
略
知识点
如图,四棱锥






(1) 求证:
(2) 在棱



(3) 求点

正确答案
见解析
解析
解:
(1)方法一:取


△

所以

又




所以



所以
方法二:连结




又



又




所以

又


(2)当点


证明如下:
取棱





所以



所以
(3)点



由(1)可知








即

在


在


边

所以

设点





所以
解得



知识点
设|








正确答案
解析
∵

∴

=

∴

=

又|

则
=
=
由
∴

∵x∈[0,1],
∴8x+1∈[1,9]。
∴

知识点
如图,在正方体


求证:(1)

(2)

正确答案
见解析
解析
证明:
(1)连结A1D,
∵ E,F分别是AD和DD1的中点,∴ EF∥AD 1。
∵ 正方体ABCD-A1B1C1D1,
∴ AB∥D1C1,AB=D1C1。
∴ 四边形ABC1D1为平行四边形,即有A1D∥BC1
∴ EF∥BC1。
又EF

∴ EF∥平面AB1D1。
(2)连结AC,则AC⊥BD。
∵ 正方体ABCD-A1B1C1D1,∴AA1⊥平面ABCD,
∴ AA1⊥BD。
又
∴ A1C⊥BD。
同理可证A1C⊥BC1。
又
知识点
如图所示,矩形长为3,宽为2,在矩形内随机撒200颗黄豆,数得落在椭圆内的黄豆数为160颗,依据此实验数据可以估计出椭圆的面积约为
正确答案
4.8
解析
略
知识点
若某几何体的三视图如图所示,则此几何体的体积是( )
正确答案
解析
略
知识点
某几何体的三视图如图所示,则该几何体的体积是
正确答案
解析
略
知识点
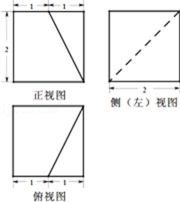
某空间几何体的三视图如图所示,则该几何体的表面积为( )
正确答案
解析
由三视图知:几何体是直三棱柱,且三棱柱的高为4,
底面是直角边长为2的等腰直角三角形,斜边长为

∴几何体的表面积S=2×



知识点
如图,在








正确答案
4
解析
略
知识点
扫码查看完整答案与解析