- 空间几何体的三视图、表面积和体积
- 共1381题
11.平面向量





正确答案
2
解析
略。
知识点
13.点



正确答案
解析
略。
知识点
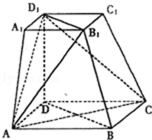
20.如图,在四棱台ABCD﹣A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.
(1)求证:B1B∥平面D1AC;
(2)求证:平面D1AC⊥平面B1BDD1.
正确答案
见解析。
解析
(1)证明:设AC∩BD=E,连接D1E,
∵平面ABCD∥平面A1B1C1D1.
∴B1D1∥BE,∵B1D1=BE=
∴四边形B1D1EB是平行四边形,
所以B1B∥D1E.
又因为B1B⊄平面D1AC,D1E⊂平面D1AC,
所以B1B∥平面D1AC
(2)证明:侧棱DD1⊥平面ABCD,AC⊂平面ABCD,
∴AC⊥DD1.
∵下底ABCD是正方形,AC⊥BD.
∵DD1与DB是平面B1BDD1内的两条相交直线,
∴AC⊥平面B1BDD1
∵AC⊂平面D1AC,∴平面D1AC⊥平面B1BDD1.
知识点
11.在平面直角坐标系xOy中,已知△ABC顶点A(﹣4,0)和C(4,0),顶点B在椭圆

正确答案
解析
利用椭圆定义得a+c=2×5=10b=2×4=8
由正弦定理得

知识点
6.在




正确答案
解析

知识点
9.在△ABC中,若|





正确答案
解析
若|



则

即有
E,F为BC边的三等分点,
则






=(



=




故选B.
知识点
3.已知向量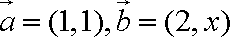

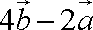
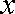
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.某三棱锥的三视图如右图所示,则该三棱锥的最长棱的棱长为__________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆



(1)求椭圆
(2)如图,过右焦点












求证: 
正确答案
见解析。
解析
(1)由条件
故所求椭圆方程为
(2)设过点


由
因为点


设点

因为直线

直线
令


所以点

直线
所以

知识点
20.如图,四棱柱ABCD﹣A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=
(1)证明:AA1⊥BD
(2)证明:平面A1BD∥平面CD1B1;
(3)求三棱柱ABD﹣A1B1D1的体积。
正确答案
见解析。
解析
(1)证明:∵底面ABCD是正方形,
∴BD⊥AC,
又∵A1O⊥平面ABCD且BD⊂面ABCD,
∴A1O⊥BD,
又∵A1O∩AC=O,A1O⊂面A1AC,AC⊂面A1AC,
∴BD⊥面A1AC,AA1⊂面A1AC,
∴AA1⊥BD
(2)∵A1B1∥AB,AB∥CD,
∴A1B1∥CD,
又A1B1=CD,
∴四边形A1B1CD是平行四边形,
∴A1D∥B1C,同理A1B∥CD1,
∵A1B⊂平面A1BD,A1D⊂平面A1BD,CD1⊂平面CD1B1,B1C⊂平面CD1B,
且A1B∩A1D=A1,CD1∩B1C=C,
∴平面A1BD∥平面CD1B1
(3)∵A1O⊥面ABCD,
∴A1O是三棱柱A1B1D1﹣ABD的高,
在正方形ABCD中,AO=1.
在Rt△A1OA中,AA1=2,AO=1,
∴A1O=
∴V三棱柱ABD﹣A1B1D1=S△ABD•A1O=


∴三棱柱ABD﹣A1B1D1的体积为
知识点
扫码查看完整答案与解析