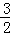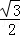- 空间几何体的三视图、表面积和体积
- 共1381题
11.在半径为1的球面上有不共面的四个点A,B,C,D且



正确答案
解析
构造一个长方体,使得四面体ABCD的六条棱分别是长方体某个面的对角线(如图).设长方体的长、宽、高分别为


考查方向
解题思路
构造法来解。
易错点
缺乏空间想象力。
知识点
16. 




正确答案
32
解析
如下图所示:


考查方向
解题思路
先求出球的半径再计算其表面积。
易错点
不会计算球的半径。
知识点
11.已知球








正确答案
解析
设球O的半径为r,球心O在平面ABC上的射影为M,则M为三角形ABC的外心,由





考查方向
解题思路
先确定M为三角形ABC外接圆的圆心;利用平面几何的知识求出球O的半径,然后带入表面积公式即可。
易错点
不知道球心O在面ABC内的射影的位置;不会构建平面几何的知识求解半径。
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
正方形

正确答案
解析
结合已知中的点E,F的位置,进行作图,推理可知,在反射的过程中,直线是平行的,那么利用平行关系,作图,可以得到回到EA点时,需要碰撞8次即可。
知识点
已知抛物线C:y2=x的焦点为F,A(x0,y0)是C上一点,|AF|=x0,x0=( )
正确答案
解析
由抛物线的定义,可得|AF|=x0+



知识点
如图,O为坐标原点,双曲线C1:


(1)求C1,C2的方程;
(2)是否存在直线l,使得l与C1交于A,B两点,与C2只有一个公共点,且
正确答案
见解析。
解析
(1)设C2的焦距为2c2,由题意知,2c2=2,2a1=2.从而a1=1,c2=1.
因为点

所以

由椭圆的定义知
于是

故C1,C2的方程分别为

(2)不存在符合题设条件的直线。
①若直线l垂直于x轴,因为l与C2只有一个公共点,所以直线l的方程为

当


所以

此时,
当

②若直线l不垂直于x轴,设l的方程为y=kx+m.
由
当l与C1相交于A,B两点时,设A(x1,y1),B(x2,y2),则x1,x2是上述方程的两个实根,从而

于是y1y2=k2x1x2+km(x1+x2)+m2=
由
因为直线l与C2只有一个公共点,所以上述方程的判别式Δ=16k2m2-8(2k2+3)(m2-3)=0.
化简,得2k2=m2-3,因此
于是
即

综合①,②可知,不存在符合题设条件的直线。
在第(1)问中,利用已知条件结合图形以及双曲线、椭圆中a,b,c的几何意义,列出关于a1,b1,a2,b2的方程,得到它们的值,从而求出双曲线C1、椭圆C2的方程;在第(2)问中,首先对直线l的斜率进行分类讨论,当斜率k不存在时易得A,B两点的坐标,进而判断满足题设条件的直线l不存在;当斜率k存在时,可先设出l的方程,然后代入曲线方程,利用根与系数的关系并结合向量的运算,依此判断满足题设条件的直线l不存在。
知识点
某几何体的三视图如下图,则几何体的体积为( )
正确答案
解析
在长方体中构造几何体

题设条件。其体积
知识点
以边长为1的正方形的一边所在所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于( )
正确答案
解析
边长为1的正方形,绕其一边所在直线旋转一周,得到的几何体为圆柱,
则所得几何体的侧面积为:1×2π×1=2π
知识点
正三棱柱ABC﹣A1B1C1的底面边长为2,侧棱长为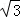
正确答案
解析
知识点
扫码查看完整答案与解析