- 抛物线的标准方程和几何性质
- 共169题
如图,在抛物线











(1)若点

(2)若

正确答案
见解析
解析
本小题主要考查抛物线的方程、圆的方程与性质、直线与圆的位置关系等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、数形结合思想、化归与转化思想,满分12分。
(1)抛物线


由点


所以点



所以
(2)设


即
由
设

由
所以

所以圆心

从而


知识点
已知函数

(1)当a=1,b=2时,求曲线

(2)设




证明:存在实数

正确答案
见解析
解析
本题主要考查函数的极值概念、导数运算法则、切线方程、导线应用、等差数列等基础知识,同时考查抽象概括、推理论证能力和创新意识。
(1)解:当a=1,b=2时,
因为f’(x)=(x-1)(3x-5)
故f’(2)=1
f(2)=0,
所以f(x)在点(2,0)处的切线方程为y=x-2
(2)证明:因为f′(x)=3(x-a)(x-
由于a<b.
故a<
所以f(x)的两个极值点为x=a,x=
不妨设x1=a,x2=
因为x3≠x1,x3≠x2,且x3是f(x)的零点,
故x3=b.
又因为

x4=


所以a,

所以存在实数x4满足题意,且x4=
知识点
如图,在直角坐标系xOy中,点P(1,

(1)求p,t的值;
(2)求△ABP面积的最大值。
正确答案
(1)
解析
(1)由题意知
(2)设A(x1,y1),B(x2,y2),因为OM过AB的中点,而且直线OM的方程为x-y=0,所以设线段AB的中点为Q(m,m)。
由题意,设直线AB的斜率为k(k≠0)。
由
所以直线AB方程为y-m=
即x-2my+2m2-m=0。
由
消去x,整理得y2-2my+2m2-m=0,
所以
从而|AB|=

设点P到直线AB的距离为d,
则
设△ABP的面积为S,
则S=

由
令u=

设S(u)=u(1-2u2),0<u≤
则S′(u)=1-6u2。
由S′(u)=0,得
所以S(u)max=
故△ABP面积的最大值为
知识点
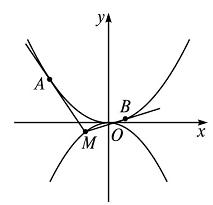
如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x0,y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x0=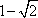
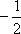
(1)求p的值;
(2)当M在C2上运动时,求线段AB中点N的轨迹方程(A,B重合于O时,中点为O)。
正确答案
见解析
解析
(1)因为抛物线C1:x2=4y上任意一点(x,y)的切线斜率为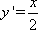
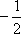
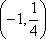
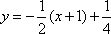
因为点M(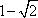
于是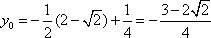
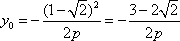
由①②得p=2.
(2)设N(x,y),A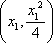
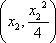
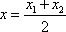
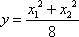
切线MA,MB的方程为
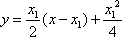
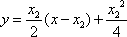
由⑤⑥得MA,MB的交点M(x0,y0)的坐标为
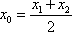
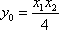
因为点M(x0,y0)在C2上,即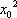
所以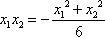
由③④⑦得
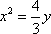
当x1=x2时,A,B重合于原点O,AB中点N为O,坐标满足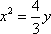
因此AB中点N的轨迹方程为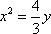
知识点
若抛物线y2=2px的焦点坐标为(1,0),则p=__________;准线方程为__________。
正确答案
2;x=-1
解析
根据抛物线定义

知识点
扫码查看完整答案与解析