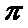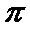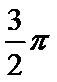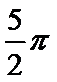- 定义法求轨迹方程
- 共97题
1
题型:填空题
|
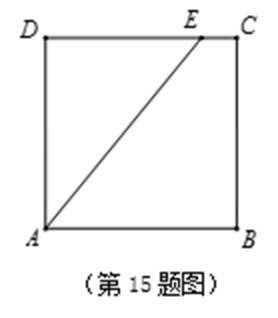
15.如图,在边长为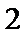
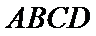
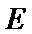
现将△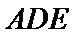
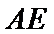
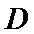
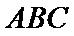

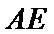
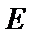
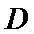
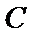
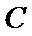
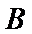
则点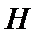
正确答案
解析
由题意,在平面AED内过点D作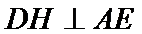
则
当E从点D运动到C,再从C运动到B,故H点的轨迹是以AD'为直径的半圆弧,
根据边长为2的正方形ABCD知圆半径是1,
所以其所对的弧长为π,
故答案为:π
考查方向
本题考查与二面角有关的立体几何综合题目,解题的关键是由题意得出点H的轨迹是圆上的一段弧,翻折问题中要注意位置关系与长度等数量的变与不变.本题是一个中档题目
解题思路
根据图形的翻折过程中变与不变的量和位置关系知,在平面AED内过点D作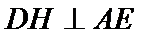
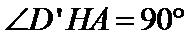
易错点
主要易错于信息的转化失败,导致计算出错
知识点
定义法求轨迹方程直接法求轨迹方程
1
题型:
单选题
|
12. 正方体ABCD—A1B1C1D1的棱长为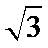
条封闭的曲线,这条曲线的长度是
正确答案
D
解析
正方体的各个面根据与球心位置关系分为两类:ABCD、AA1DD1、AA1BB1为过球心的截面,截痕为大圆弧,各弧圆心角为60度,所以根据弧长公式可以求得
考查方向
正方体的结构特征
解题思路
找到正方体的外接圆的圆心和半径,实际上是求球在正方体各个面上交线的长度计算。
易错点
空间想象能力和计算能力
知识点
棱柱的结构特征定义法求轨迹方程
下一知识点 : 相关点法求轨迹方程
扫码查看完整答案与解析