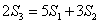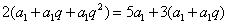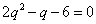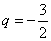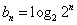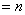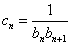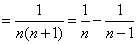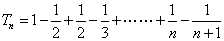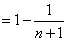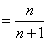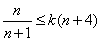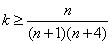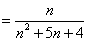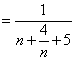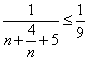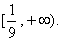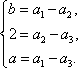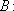- 由数列的前几项求通项
- 共480题
已知各项均为正数的等比数列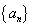
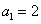
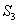
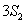
(1)求数列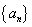
(2)设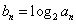
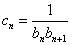
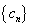
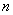
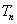
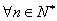
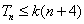
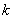
正确答案
见解析。
解析
(1)
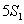
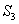
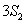

即
化简得
解得: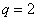
因为数列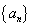
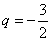
所以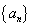
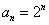
(2)由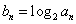




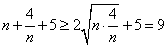
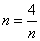
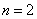


知识点
如图,已知抛物线




















给出下列三个结论:
① 数列
② 对

③ 若


其中,所有正确结论的序号是_____。
正确答案
①②③
解析
略
知识点
已知椭圆

正确答案
解析
略
知识点
已知数列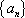
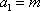
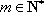
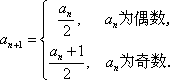
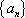

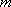
正确答案
8
解析
略
知识点
对于数列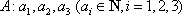
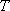
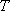
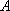
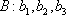
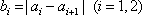
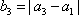
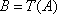
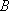
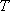
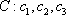

(1)试问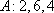
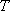
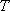
(2)设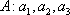
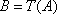
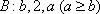
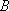
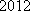
(ⅰ)求
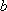
(ⅱ)若数列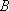
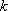
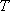
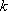
正确答案
见解析
解析
(1)解:数列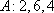
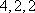
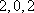
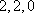
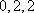
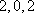
以下重复出现,所以不会出现所有项均为
(2)解:(ⅰ)因为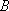
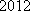
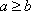

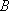
所以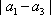
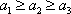

当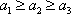
由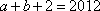
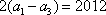
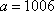
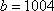
当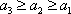
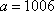
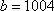
(ⅱ)方法一:由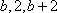
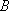
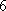
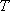
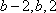
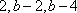
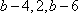
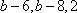
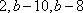
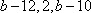
由此可见,经过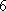
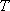
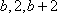
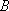
因为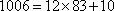
所以,数列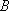
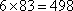
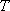
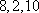
接下来经过“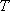
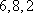
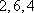
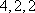
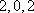
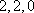
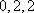
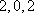
从以上分析可知,以后重复出现,所以数列各项和不会更小。
所以经过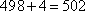
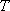
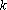
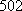
方法二:若一个数列有三项,且最小项为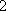
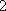
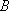
若数列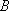
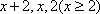
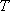
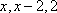
所以与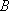
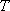
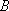
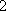
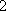
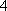
因此,数列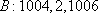
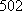
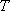
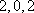
通过列举,不难发现各项为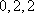
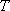
所以,至少通过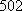
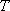
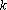
知识点
扫码查看完整答案与解析