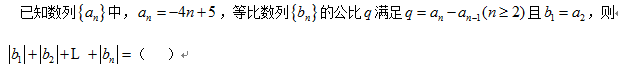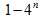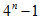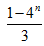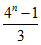由数列的前几项求通项
共480题

· 由数列的前几项求通项

由数列的前几项求通项
共480题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 13 分

对于实数，将满足“且为整数”的实数称为实数的小数部分，用记号表示，例如对于实数，无穷数列满足如下条件：

，其中

（1）若，求数列的通项公式；

（2）当时，对任意的，都有，求符合要求的实数构成的集合；

（3）设（是正整数，与互质），对于大于的任意正整数，是否都有成立，证明你的结论。

正确答案

见解析

解析

（1），，，，

所以 ……………………………………4分

（2），则，从而

则所以

解得：（，舍去） ……………….6分

所以集合 . ………………………………………7分

（3）结论成立. ……………………………………………8分

易知是有理数，所以对一切正整数，为0或正有理数，

设（是非负整数，是正整数，且互质）

由，可得； …………………………………9分

若，设（，是非负整数）

则，而由得

，故，，可得 ………11分

若则，

若均不为0，则这个正整数互不相同且都小于，但小于的正整数共有个，矛盾.

故中至少有一个为0，即存在，使得.

从而数列中以及它之后的项均为0，所以对于大于的自然数，都有 …………13分

知识点

由数列的前几项求通项

题型：单选题

单选题 · 5 分

在数列中，则的值为（）

D16

正确答案

解析

略

知识点

由数列的前几项求通项

题型：简答题

简答题 · 14 分

设数列的前n项和为，已知，是数列的前n项和.

(1)求数列的通项公式；

(2)求；

(3)求满足的最大正整数n的值.

正确答案

见解析。

解析

知识点

由数列的前几项求通项

题型：单选题

单选题 · 5 分

正确答案

解析

略

知识点

由数列的前几项求通项

题型：填空题

填空题 · 5 分

已知是等差数列的前项和，其中

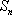
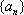
正确答案

6；9

解析

略

知识点

由数列的前几项求通项

继续学习学习下一知识点

下一知识点 : 由an与Sn的关系求通项an

百度题库 > 高考 > 文科数学 > 由数列的前几项求通项

扫码查看完整答案与解析